B8 - 2D boundary value problem

most of the formulation is a natural extension of a 1D problem:
a square grid with equal spacing, $Δ x = Δ y$
considering a vanishing lapalican of a scalar:

\nabla^{2} T = \frac{\partial^{2} T}{\partial x^{2}} + \frac{\partial^{2} T}{\partial y^{2}}

on a square grid, the second derivatives are evaluated separately in each direction
assuming $Δ x = Δ y$ , the finite difference is:

\nabla^{2} T |_{j, p} = \frac{T_{j - 1, p} + T_{j + 1, p} + T_{j, p - 1} + T_{j, p + 1} - 4 T_{j, p}}{(Δ x)^{2}}

thinking in terms of $N \times M$ matrices, when in physical space
elements of the right matrix have 5 coefficients each

image: B Hnat, lecture notes

just as for a 1D problem, writing a matrix equation, where linear algebra based solvers can be applied for numerical solutions
so a column vector for $T$ must be constructed
taking $j$ in $[0, J - 1]$ and $p$ in $[0, P - 1]$ , giving $J \cdot P$ grid points, equations and unknowns
mapping each unknown to a column index and each equation to a row index
a single index is needed to number points on a 2D grid

k = j \cdot P + p, 0 \leq k \leq K = J \cdot P

this is called row-major indexing scheme, which is standard in C
a single memory block is allocated by malloc

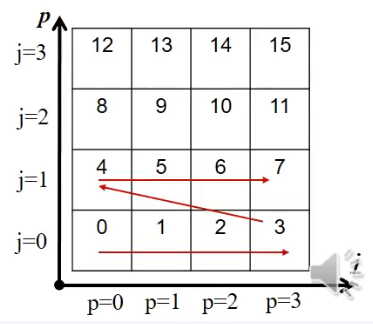
image: B Hnat, lecture notes

the matrix is tridiagonal, that can be symbolically drawn as:

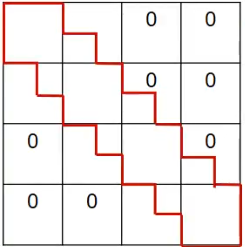
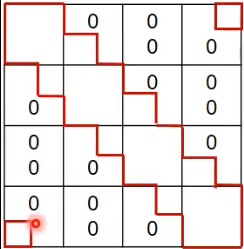
image: B Hnat, lecture notes

each rectangle is either all zeros, a diagonal matrix, or a banded matrix
for periodic boundary conditions, there will be nonzero values in the corners
this is tackled using the same folding approach as in 1D

k = q (j, p) \cdot P + p, 0 \leq k \leq J \cdot P