B7 - boundary conditions

types of boundary conditions

dirichlet boundary conditions: fixed boundary value, eg: $y (x_{b}, t) = C (t)$
von neumann boundary conditions: zero or fixed gradient, eg: $y^{'} (x_{b}, t) = 0$ or $D (t)$
periodic boundary conditions on $x$ domain of length, $L$ , such that $y (x + L) = y (x)$

evaluating a second derivative for von neumann BC in space at a left boundary, $x_{0}$
the taylor expansion:

f (x_{0} + Δ x) \approx f (x_{0}) + f^{'} (x_{0}) Δ x + \frac{1}{2} f^{″} (x_{0}) (Δ x)^{2} + O [(Δ x)^{3}]

f (x_{1}) = f (x_{0} + Δ x) \approx f (x_{0}) + \frac{1}{2} f^{″} (x_{0}) (Δ x)^{2}

f^{″} (x_{0}) = \frac{2}{(Δ x)^{2}} [f (x_{1}) - f (x_{0})]

f^{″} (x_{0}) = \frac{f (x_{1}) + f (x_{- 1}) - 2 f (x_{0})}{(Δ x)^{2}}

f^{'} (x_{0}) = \frac{1}{2 Δ x} [f (x_{1}) - f (x_{- 1})] = 0 ⟹ f (x_{1}) = f (x_{- 1})

f^{″} (x_{0}) = \frac{2}{(Δ x)^{2}} [f (x_{1}) - f (x_{0})]

\frac{d T}{d t} = \frac{d^{2} T}{d x^{2}} + S (x)

\frac{1}{(Δ x)^{2}} [T_{k - 1} + T_{k + 1} - 2 T_{k}] + S_{k} = 0

\frac{A}{(Δ x)^{2}} [\begin{matrix} T_{0} \\ ⋮ \\ T_{K - 1} \end{matrix}] = - [\begin{matrix} S_{0} \\ ⋮ \\ S_{K - 1} \end{matrix}]

\frac{1}{(Δ x)^{2}} [T_{k - 1} + T_{k + 1} - 2 T_{k}] = - S_{k}

approach 1: the domain is discretised by $K + 1$ points with boundaries at $x_{0}$ and $x_{K}$ , where $T_{0} = T_{K} = 0$

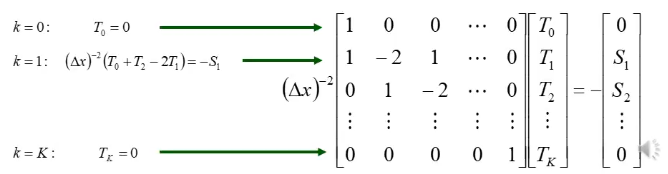
image: B Hnat, lecture notes

approach 2: the domain is discretised by $K$ points, with boundaries at 'ghost' points, $x_{- 1}$ and $x_{K}$ , with dirichlet BCs: $T_{- 1} = T_{K} = 0$ , using which the equations for 'real' grid pints are simplified

image: B Hnat, lecture notes

the matrix is sparse (many 0's) and banded (non-zero elements near the diagonal), which can be easily inverted
only the non-zero elements are needed for matrix inversion, and only these should be stored in the memory
once solution is found, the original matrix is needed to match the value to a correct grid point
this requires a formula that gives a row number of a non-zero element for a given column, $j$
suppose a reduced matrix, $B$ , which contains only the non-zero elements, such that:

a_{i j} = b_{[k_{u} + i - j] j}

$k_{u}$ is a constant added to assure that the row index is always $> 0$ , which is equal to the number of non-empty bands above/below the diagonal

image: B Hnat, lecture notes

note: arrays are always stored in 1D, so a 2D array, b[i][j] in C is translated to a single index of an element in a memory block

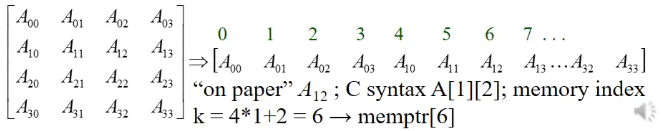
image: B Hnat, lecture notes

\frac{d^{2} T}{d x^{2}} = - S (x)

the periodic $x$ domain has a length $L$ , such that any solution satisfies: $T (x + L) = T (x)$ and $S (x + L) = S (x)$
representing the function at $K$ grid points: $x_{K} = (k L) / K$ , $0 \leq k \leq K$
the periodic boundary implies that:

\begin{matrix} T (x_{0} - Δ x) = T (x_{0} - Δ x + L) = T [x_{0} + (L - Δ x)] \\ or, T_{- 1} = T_{K - 1} \end{matrix}

\frac{1}{(Δ x)^{2}} [T_{- 1} + T_{1} - 2 T_{0}] = - S_{0} ⟹ \frac{1}{(Δ x)^{2}} [T_{- K - 1} + T_{1} - 2 T_{0}] = - S_{0}

T^{″} |_{k = 0} = \frac{1}{(Δ x)^{2}} [T_{K - 1} + T_{1} - 2 T_{0}] = S_{0}

T^{″} |_{k = K - 1} = \frac{1}{(Δ x)^{2}} [T_{K - 2} + T_{0} - 2 T_{K - 1}] = S_{K - 1}

{(\frac{1}{Δ x})}^{2} [\begin{matrix} - 2 & 1 & 0 & \dots & 1 \\ 1 & - 2 & 1 & \dots & 0 \\ 0 & 1 & - 2 & \dots & 0 \\ ⋮ & ⋮ & ⋮ & ⋱ & ⋮ \\ 1 & 0 & 0 & \dots & - 2 \end{matrix}] [\begin{matrix} T_{0} \\ T_{1} \\ T_{2} \\ ⋮ \\ T_{K - 1} \end{matrix}] = - [\begin{matrix} S_{0} \\ S_{1} \\ S_{2} \\ ⋮ \\ S_{K - 1} \end{matrix}]

the matrix is sparse, but not banded due to the ones outside the near-diagonal band
this can be converted into a banded matric by changing the indices of the unknowns

thinking of it as folding of $x$ domain, so the ends of the domain are at two neighbouring points

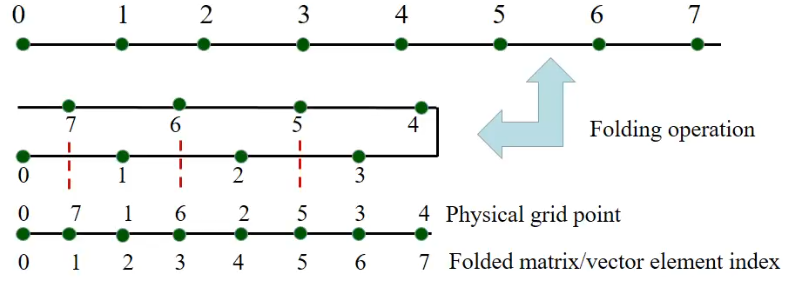
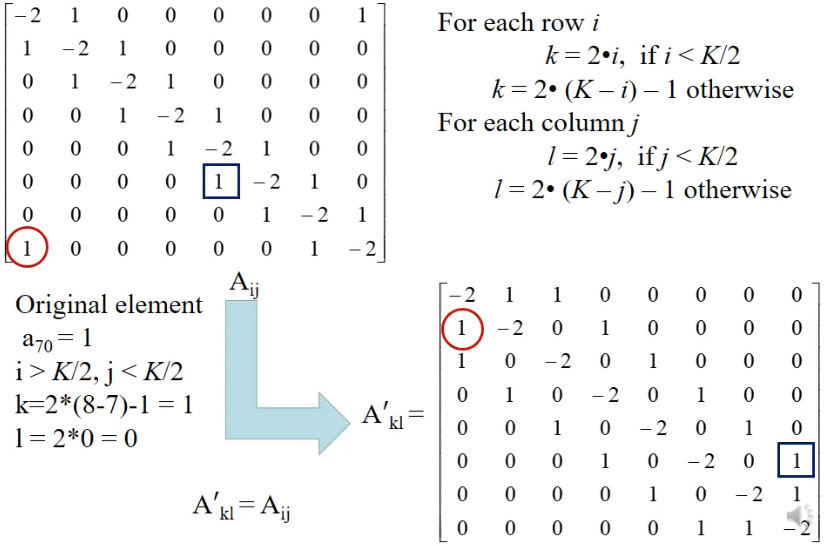
image: B Hnat, lecture notes

constructing an indexing function that converts between physical locations on the grid and the index of the folded matrix such that for $K$ , the physical location indexed by $i$ , there is the matrix element index $j (i) :$

\begin{matrix} j (i) = 2 i for i < K / 2 \\ j (i) = 2 (K - i) - 1 otherwise \end{matrix}

then: $T_{j (i)}^{'} = T_{i}$ , $S_{j (i)}^{'} = S_{i}$ and $A_{j (i) j (k)}^{'} = A_{i k}$
the benefits of folding:
- the new matrix, $A^{'}$ , does not have entries far from the diagonal
- the time to invert a matric scales as $N^{3}$ for a full matrix, but $M^{2} N$ for a banded matrix with $M$ -elements band
so $A^{'} T^{'} = S^{'}$ is solved, and $T^{'}$ is reordered each time the physical grid based $T$ is needed
the indexing function $j (i)$ is used each time the matrix/vector is accessed explicitly