B6c - upwinding

this is a simpler solution, inspired by method of characteristic
it involves looking along the line on which a PDE can be transformed into an ODE and solved
here, looking at the direction which contributes to the solution at $k$ , ie. the direction of the advection velocity vector
the solution at $x (t)$ depends on the grid point to the left
for a continuous equation, the solution is found by examining the lines on which the solution takes a constant value
on a grid, since one cannot look along the continuous line, the solution at some point, $(t_{j}, x_{k})$ , depends on the data arriving from the 'left' of $x_{k}$ on the grid, which reflects the direction of propagation, $\vec{v}$

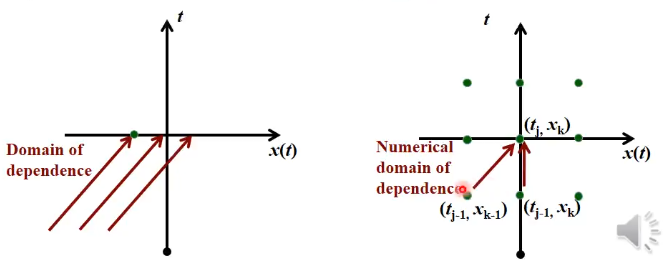
image: B Hnat, lecture notes

the domain of influence for a single constant advection speed is a straight line

\begin{matrix} \frac{y_{k}^{j + 1} - y_{k}^{j}}{Δ t} + \frac{v}{Δ x} (y_{k}^{j} - y_{k - 1}^{j}) = 0 for v > 0 \\ \frac{y_{k}^{j + 1} - y_{k}^{j}}{Δ t} - \frac{v}{Δ x} (y_{k}^{j} - y_{k - 1}^{j}) = 0 for v < 0 \end{matrix}

the method is stable if information travels no more than one grid cell in one time step: $v (Δ t) / (Δ x) < 1$ , which is called the courant-friedrichs-lewy (CFL condition)
this is necessary for convergence of many hyperbolic PDEs
it is first order in time and in space