B6b - finite difference

spatial discretisation uses centred method, forward time centred space (FTCS) scheme

\frac{y_{k}^{j + 1} - y_{k}^{j}}{Δ t} + \frac{v}{2 Δ x} (y_{k + 1}^{j} - y_{k - 1}^{j}) = 0

using the same fourier method as before, it can be shown that this scheme is consistent in time
but it needs to be shown that this is stable
the plane wave solution exists, so analytically, it is stable
using fourier representation:

y_{k}^{j} = \sum_{m = 0}^{M - 1} \exp (i \frac{2 π Δ x}{L} m k) {\bar{y}}_{m}^{j}

where, ${\bar{y}}_{m}^{j}$ are fourier amplitudes of each mode, $m$

considering one mode: $y_{k}^{j} = \exp (i m q_{0} k) {\bar{y}}_{m}^{j}$

{\bar{y}}_{m}^{j + 1} = {\bar{y}}_{m}^{j} [1 - \frac{v Δ t}{2 Δ x} (e^{i m q_{0}} - e^{- i m q_{0}})] = {\bar{y}}_{m}^{j} [1 - \frac{v Δ t}{Δ x} i \sin (m q_{0})]

the amplification factor, which is the ratio of fourier amplitudes at $j + 1$ and $j$ needs to be found to see if the mode is growing or decaying

| \frac{{\bar{y}}_{m}^{j + 1}}{{\bar{y}}_{m}^{j}} | = 1 + {(\frac{v Δ t}{Δ x})}^{2} \sin^{2} (m q_{0})

when $\sin (m q_{0}) = 1$ , there is instability
since the $R H S > 1$ , the scheme is unstable
the most unstable mode is when $m q_{0} = π / 2$
a solution would be to take a very small $Δ t$ , which is impractical
however, a small damping can be added

damping

\frac{\partial y}{\partial t} + v \frac{\partial y}{\partial x} - γ \frac{\partial^{2} y}{\partial x^{2}} = 0

the artificial last term needs to be sufficiently small so that the scheme is consistent
$γ$ must scale with $Δ x$ and $Δ t$

\begin{matrix} {\bar{y}}_{m}^{j + 1} = {\bar{y}}_{m}^{j} [1 - \frac{v Δ t}{2 Δ x} (e^{i m q_{0}} - e^{- i m q_{0}}) + \frac{γ Δ t}{(Δ x)^{2}} (e^{i m q_{0}} + e^{- i m q_{0}} - 2)] \\ | g | = {[1 + \frac{2 γ Δ t}{(Δ x)^{2}} (\cos (m q_{0}) - 1)]}^{2} + {(\frac{v Δ t}{Δ x})}^{2} \sin^{2} (m q_{0}) \end{matrix}

this can be analysed graphically

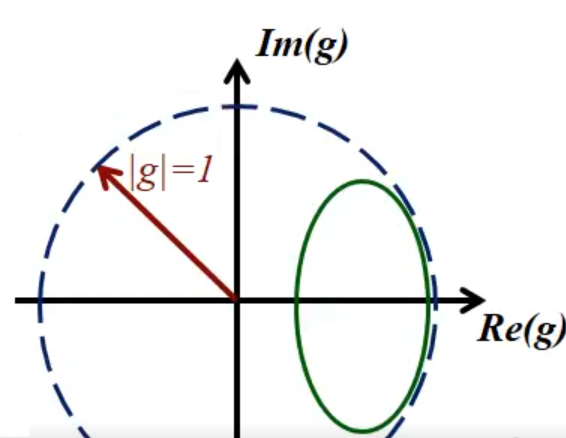
image: B Hnat, lecture notes

the wanted complex amplification factor, $| g | < 1$ , is within the blue dashed circle
for a given $γ$ , $g$ is an ellipse
the important behaviour is near $I m (g) = 0$
got the green ellipse to be within enclosed within the blue circle, their curvatures near $R e (g) = 1$ need to be matched for small $m q_{0}$
the small $m q_{0}$ limit is found using taylor expansion of $\cos$ and $\sin$ around $x = 0 :$

\begin{matrix} \cos x \approx 1 - \frac{1}{2} x^{2} \\ \sin x \approx x \\ | g | \approx 1 + (m q_{0})^{2} [{(\frac{v Δ t}{Δ x})}^{2} - \frac{2 γ Δ t}{(Δ x)^{2}}] \end{matrix}

for $g < 1$ , the second term in the square bracket must be greater than the first:

2 γ \geq v^{2} Δ t

this approach of adding a sufficiently large damping is called lax-wendroff scheme
unfortunately, it generates false oscillations near sharp features, which can cause problems, especially for strictly positive quantities