B3 - local truncation error

local truncation error

the local error at a particular grid point due to discrete representation of the derivative

{\hat{y}}_{k}^{j + 1} = Q_{k}^{j} ({\hat{y}}_{o}^{j}, {\hat{y}}_{1}^{j}, \dots, {\hat{y}}_{N - 1}^{j})

the function, $Q_{k}$ , gives a solution at time step, $j + 1$ , based on solution at all special grid points at a current time, $j$
for example, the first order ODE:

\begin{matrix} Q_{k}^{j} = f (x_{k}, t^{j}) + Δ t F (x_{k}, t^{j}) \\ {\hat{y}}_{k}^{j} = f (x_{k}, t^{j}) \end{matrix}

L T E \equiv Q_{k} [y (x_{0}, t_{j}), y (x_{1}, t_{j}), \dots, y (x_{N - 1}, t_{j})] - y (x_{k}, t_{j + 1})

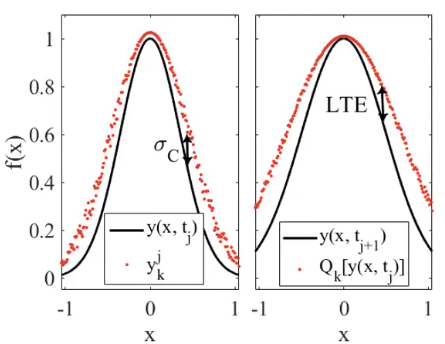
image: B Hnat, lecture notes

$σ_{C}$ compares a numerical and the analytical solutions at a fixed time and a given point
LTE evolves the analytic solution from time $j$ to $j + 1$ , and then compares the evolved solution to the analytic one at time $j + 1$
the order of a numerical method measures the change in error of a numerical solution as step size is decreased
the scheme has order, $N$ , in time and, $M$ , in space if and only if for any smooth solution of initial value problem, the following relation is true for some values $C_{0}$ and $C_{1} :$

∥ L T E ∥ < C_{0} (Δ x)^{M + 1} + C_{1} (Δ t)^{N + 1}

so, the error decreases as $Δ x$ and $Δ t$ are decreased
eg: if $M = N = 1$ , decreasing $Δ x$ and $Δ t$ by $2$ decreases LTE by a factor of $4$
higher order scheme converge faster when the grid is made finer
the scheme is consistent if it has an order of at least $1$ in each direction (ie. $M, N \geq 1$ )
eg: considering an initial value problem given by an ODE with analytical solution, $f_{a}$ , and the finite difference scheme:

\begin{matrix} \frac{d f}{d t} = f^{'} = G (t) \\ f^{j + 1} = f^{j} + Δ t G (t^{j}) ⟹ Q^{j} \equiv f^{j} + Δ t G^{j} \\ L T E = Q^{j} [f_{a} (t^{j})] - f_{a} (t^{j + 1}) = f_{a} (t^{j}) + Δ t G_{a} (t^{j}) - f_{a} (t^{j + 1}) \end{matrix}

\begin{matrix} L T E = f_{a} (t^{j}) + Δ t G_{a} (t^{j}) - \sum_{n = 0}^{\infty} \frac{f_{a}^{n} (t^{j})}{n!} (Δ t)^{n} \\ ⋮ \\ | L T E | = | - \frac{1}{2} f_{a}^{″} (t^{j}) (Δ t)^{2} + O (Δ t)^{3} | \end{matrix}

stability

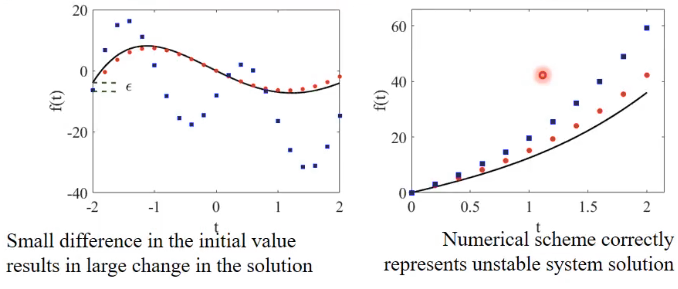
image: B Hnat, lecture notes

introducing a small error, $ϵ$ , in the system
the numerical solution must stay closed to the unperturbed ones
if the exact system is unstable, the divergence between trajectories should become small in relative terms as $Δ t \to 0$
the numerical solution will still grow, but must do so at the correct growth rate of the system