A3 - form factor

assuming a homogenous particles (uniform electron density)
each electron is a secondary wave source described as $a \exp (i ϕ)$
the amplitude, $a$ , is the same for all electrons, but $ϕ$ is position-dependent
the resulting wave amplitude is:

A = \sum_{i} a_{i} \exp (i ϕ_{i})

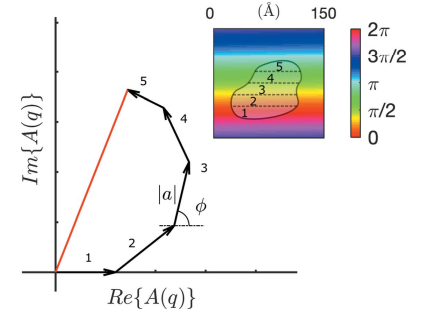
image: CJ Gommes, S Jakschb and S Frielinghausb (2021)

I (q) = {| ∭_{p a r t i c l e} \exp (i q y) ρ d x d y d z |}^{2}

where, $ρ$ is the electron density

detectors measure intensity, not amplitude: $I = | A |^{2}$
for small $q$ , $λ^{*} = 2 π / q ≫ λ$ , so all scattering centres scatter in phase
- all arrows point in the same direction, maximising $I$
for large $q$ , $λ^{*} < λ$ , so different parts of the particle scatter out of phase
- arrows point in different directions, lowering $I$
the transition from plateau (small $q$ ) to oscillatory decrease occurs where $2 π / q \sim λ$
the form factor is the intensity scattered by an individual nanoparticle over a complete range of $q$
customarily, the effect of $ρ$ and $V$ are factored out, so the form factor $P (q)$ is defined as:

I (q) = ρ^{2} V^{2} P (q)

for small $q$ , $P (q) = 1$
this can be used to calculate the form factors of various spheres
naturally particles are modelled as sphere of radius, $R$ , with their form factors:

P (q) = {[3 \frac{\sin (q R) - q R \cos (q R)}{q R^{3}}]}^{2}

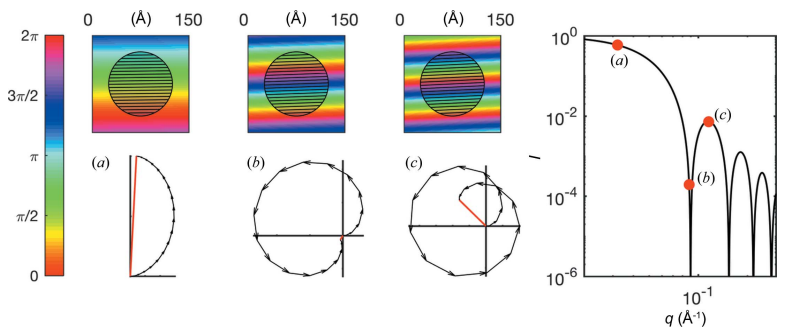
image: CJ Gommes, S Jakschb and S Frielinghausb (2021)

for nonidentical nanoparticles, the conditions for constructive and destructive interference differ, giving rise to sharp oscillations
the progressive onset of destructive interference for small $q$ obeys guinier's law:

P (q) ≃ \exp [- \frac{(q R_{G})^{2}}{3}]

where, $R_{G}$ is the radius of gyration

plotting $\ln [I (q)]$ against $q^{2}$ often yields a linear trend at low $q$ , with slope $- R_{G}^{2} / 3$
obtained $R_{G}$ can be used for an intuitive understanding of particle size
increasing $q$ beyond the validity limit of guinier's law leads to power laws of the type:

I ≃ q^{- α}

image: CJ Gommes, S Jakschb and S Frielinghausb (2021)

the specific case of $α = 4$ is porod's law, for structures with clear-cut interfaces