PX285 - L7 - boundary layers

when reynold's number, $R e$ , is large, the boundary layers are thin:

\frac{δ}{d} = {(\frac{μ}{ρ u_{0} d})}^{1 / 2} = \frac{1}{\sqrt{R e}}

typically, $R e ≫ 1$ , and the boundary layers are thin compared to the object size
considering the flow around a cylinder, where the flow outside the boundary layer can be taken to be potential

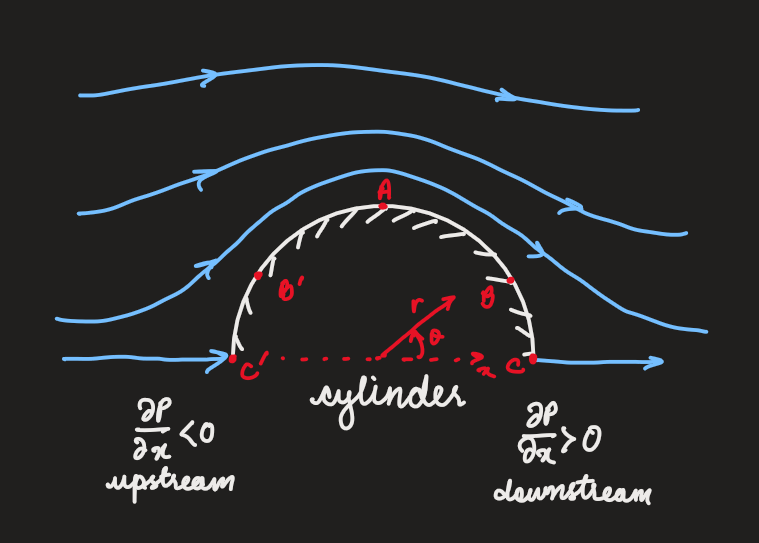
the pressure on the surface:

\begin{matrix} P_{s} (θ) = P_{0} + \frac{1}{2} ρ u^{2} (1 - 4 \sin^{2} θ) \\ P_{C^{'}} > P_{B^{'}} > P_{A} \\ P_{C} > P_{B} > P_{A} \end{matrix}

in fluids:

F \propto - \frac{\partial P}{\partial x}

in the upstream region, the pressure gradient accelerates the flow, ie. favourable pressure gradient
in the downstream region, the pressure gradient decelerates the flow, ie. adverse pressure gradient

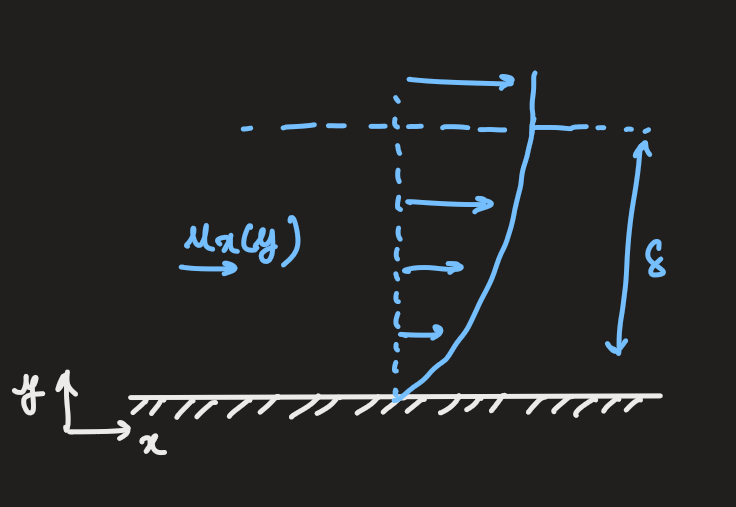
considering the flow near the surface, ie. in the boundary layer, using the navier stoke equation:

(\vec{u} \cdot \vec{\nabla}) \vec{u} = - \frac{1}{ρ} \vec{\nabla} P + \frac{μ}{ρ} \nabla^{2} u

let the density be constant
using the symmetry of the model:

u_{x} \frac{\partial u_{x}}{\partial x} = - \frac{1}{ρ} \frac{\partial P}{\partial x} + \frac{μ}{ρ} \frac{\partial^{2} u_{x}}{\partial y^{2}}

within the boundary layer: $R e$ is small, so the viscous term $≫$ inertial term

\frac{\partial^{2} u_{x}}{\partial y^{2}} = \frac{1}{μ} \frac{\partial P}{\partial x} = A (x)

since there is no acceleration in $x$

integrating twice:

⟹ u_{x} = A (x) \frac{y^{2}}{2} + B y + C

the boundary conditions:

\begin{matrix} no slip: u_{x} (y = 0) = 0 \\ potential flow: u_{x} (y = δ) = u_{0} \\ ⟹ C = 0 \end{matrix}

using the second condition:

A \frac{δ^{2}}{2} + B δ = u_{0} ⟹ B = \frac{u_{0}}{δ} - A \frac{δ}{2}

u_{x} (y) = - \frac{A}{2} (y δ - y^{2}) + \frac{u_{0}}{δ} y

this works only for $y < δ$ , therefore, $(y δ - y^{2})$ and $y / δ > 0$
if $A < 0 : u_{x} > 0$ (flow from left to right)
if $A > 0$ and sufficiently large: $u_{x} < 0$ (flow from right to left, only in the boundary layer)

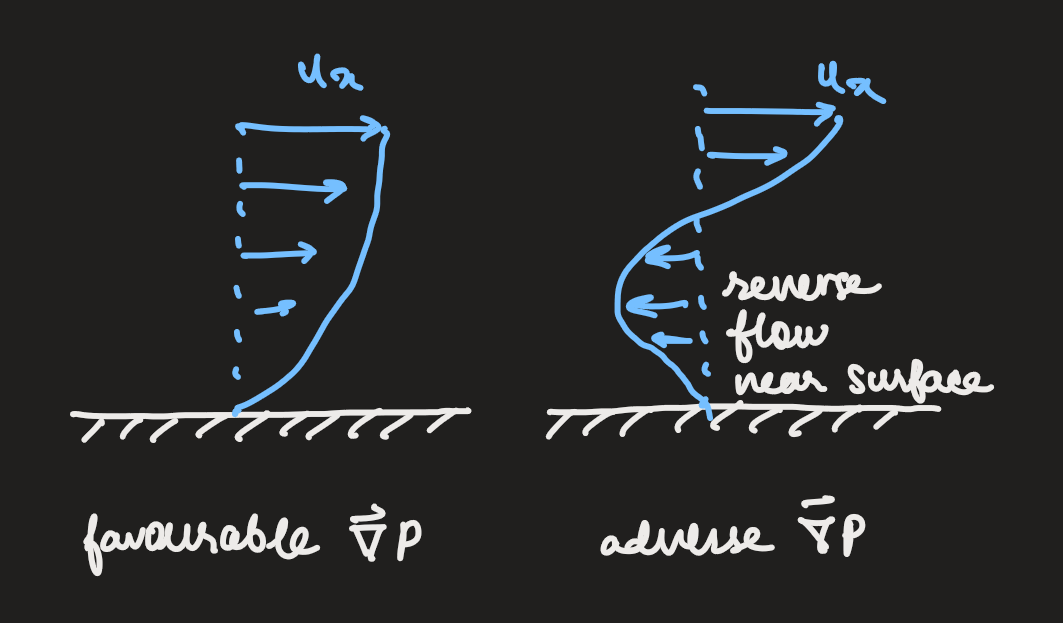
the location along the plate where the flow reverses, ie. $\partial_{y} u_{x} = 0 :$

\begin{matrix} \frac{\partial u_{x}}{\partial y} = - \frac{A}{2} (δ - 2 y) + \frac{u_{0}}{δ} = 0 \\ - \frac{A δ}{2} + \frac{u_{0}}{δ} = 0 \\ ∴ A = \frac{2 u_{0}}{δ^{2}} \end{matrix}

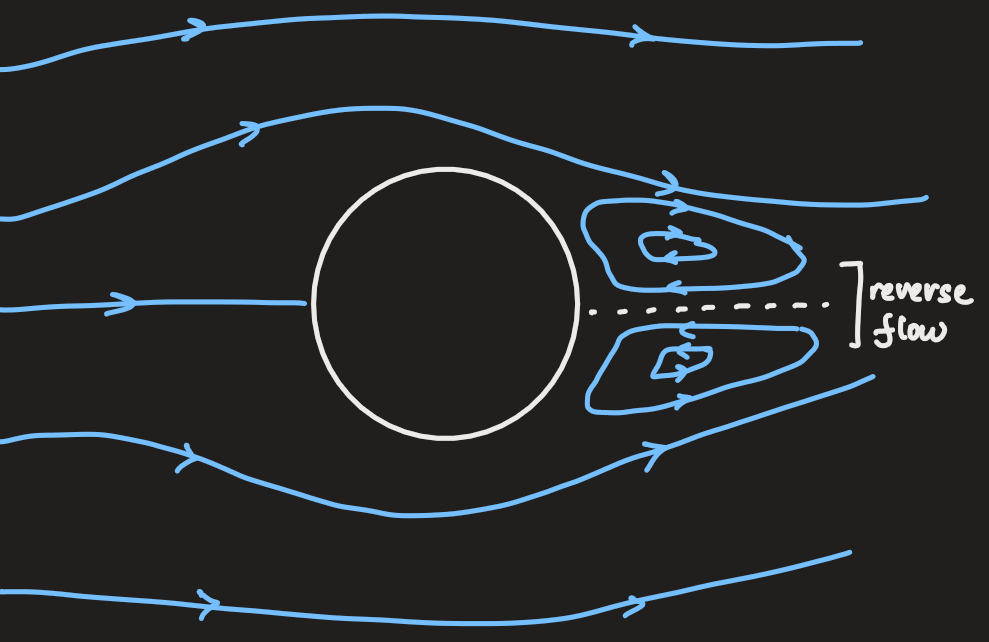
this is called the 'separation point'

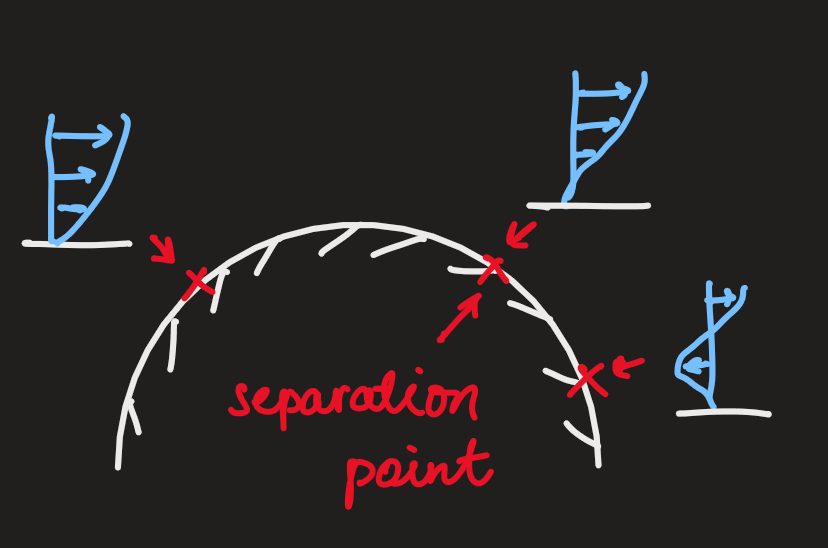
this splitting of the flow due to the flow reversal effect affects the flow outside the boundary layer
this is called boundary separation
a similar example:

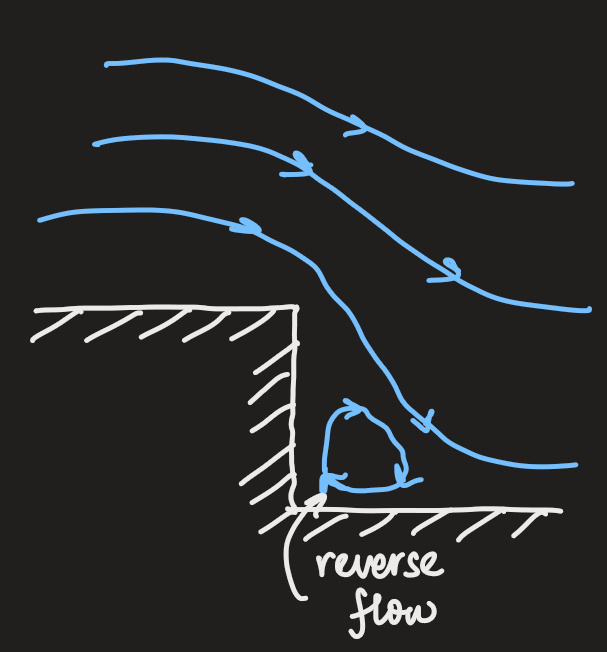
incorporating this for the flow around the cylinder: