PX285 - L6 - potential flow over a wing
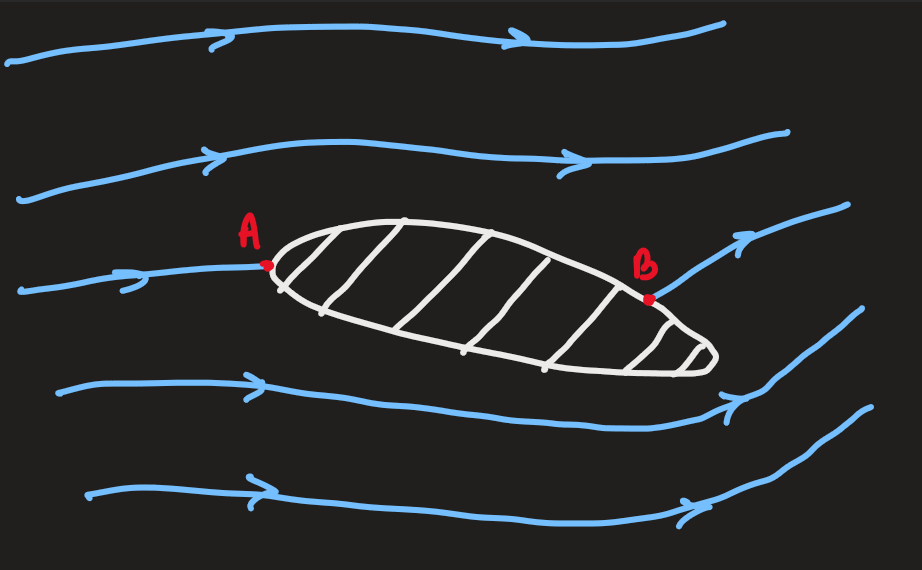
- everywhere except the transition region, the flow is irrotational, incompressible, and follows the laplace equation
- since the shape is complex, it is not analytically tractable
- numerically solving the laplace equation around the aerofoil:
- the boundary conditions:
at the surface, ie: ; , far from the aerofoil - at
, since it is incompressible: , so the net lift by magnus effect is zero - using a wind tunnel to measure the flow once it has reached a steady state, it is found that the stagnation point,
, lies on the trailing edge
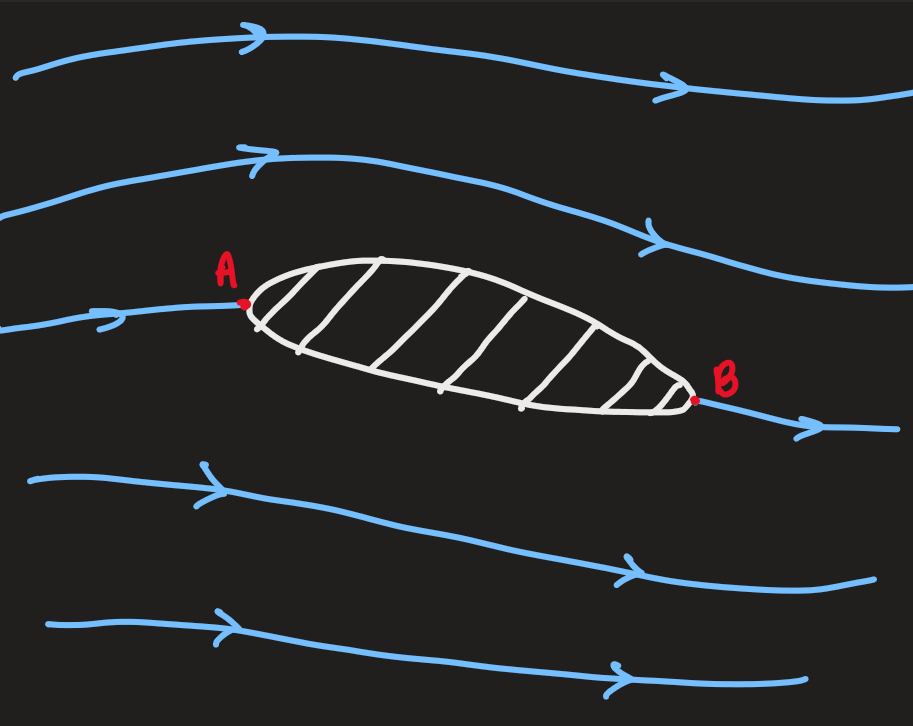
- since there are differences in speeds, and hence pressure, there will be a lift force
- this mismatch is caused by the need for considering the transition region
- the transition (or boundary) region (or layer) near an object:
can be moved from the potential flow pattern to the trailing edge by adding a circulation to the flow around the wing:
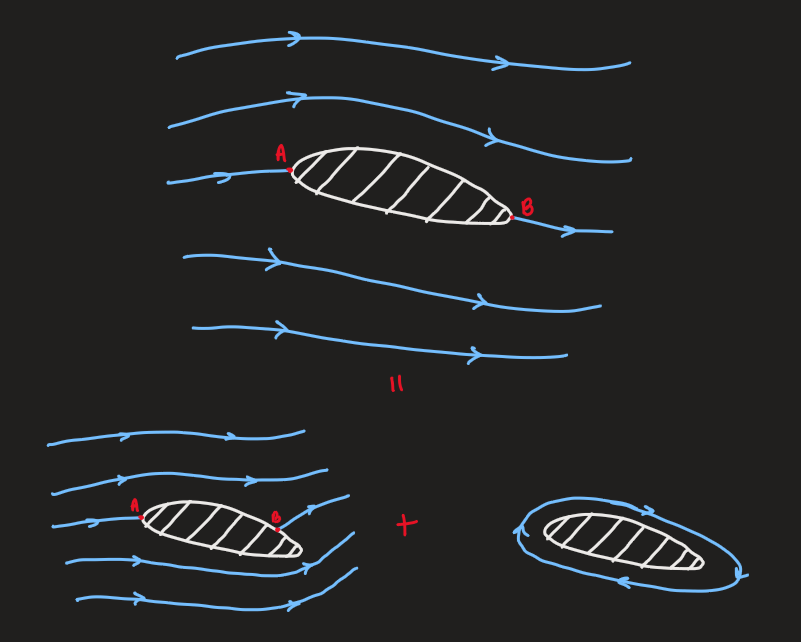
- equivalently, a circulation of the opposite sign can be subtracted
- this is called vortex shedding