PX285 - L1 - potential flows

considering a flow that is irrotational, ie: $\vec{\nabla} \times \vec{u} = 0$ , and incompressible, ie: $\vec{\nabla} \cdot \vec{u} = 0$
$\vec{u} = \vec{\nabla} ϕ$ , where $ϕ$ is the scalar potential

\begin{matrix} \vec{\nabla} \times (\vec{\nabla} ϕ) = 0 \\ \vec{\nabla} \cdot (\vec{\nabla} \cdot ϕ) = \nabla^{2} ϕ = 0 \end{matrix}

the flow is described by a scalar, and the solutions to the laplacian can be added to give a more complex solution

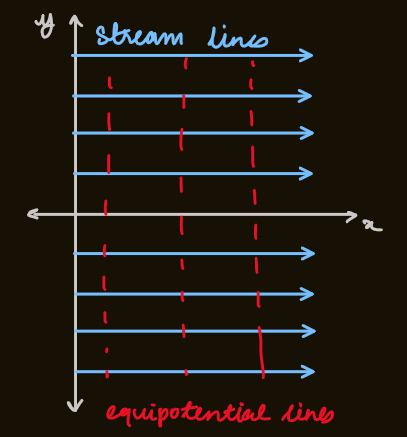
uniform flow

considering $\vec{u} = v \hat{i}$
by symmetry:

\begin{matrix} \vec{u} = \vec{\nabla} ϕ = \frac{\partial ϕ}{\partial x} \\ ⟹ ϕ = u x + c \end{matrix}

equipotential lines are lines of constant $ϕ$ , which are locally perpendicular to the stream lines
in 3D, equipotential surfaces

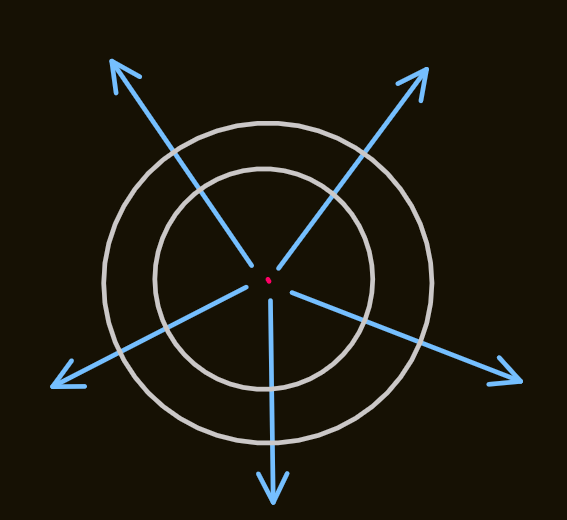
2D point source

considering a 2D point source velocity in cylindrical coordinates:

\vec{u} = \frac{q}{2 π r} \hat{r}

checking for rotation:

\vec{\nabla} \times \vec{u} = \frac{1}{r} | \begin{matrix} \hat{r} & r \hat{θ} & \hat{z} \\ \frac{\partial}{\partial r} & \frac{\partial}{\partial θ} & \frac{\partial}{\partial z} \\ u_{r} & r u_{θ} & u_{z} \end{matrix} | = 0

checking for incompressibility:

\vec{\nabla} \cdot \vec{u} = \frac{1}{r} \frac{\partial r u_{r}}{\partial r} + 0 = \frac{1}{r} (\frac{q}{2 π r} - r \frac{\partial}{\partial r} (\frac{q}{2 π r^{2}})) = 0

since the flow is incompressible and irrotational, $\vec{u} = \vec{\nabla} ϕ :$

\begin{matrix} \vec{\nabla} ϕ = \frac{q}{2 π r} \hat{r} = \frac{\partial ϕ}{\partial r} \hat{r} = \frac{q}{2 π r} \\ ⟹ ϕ = \frac{1}{2 π} \ln (r) + c = \frac{1}{4 π} \ln (r^{2}) + c \\ ∴ ϕ = \frac{1}{4 π} \ln (x^{2} + y^{2}) + c \end{matrix}

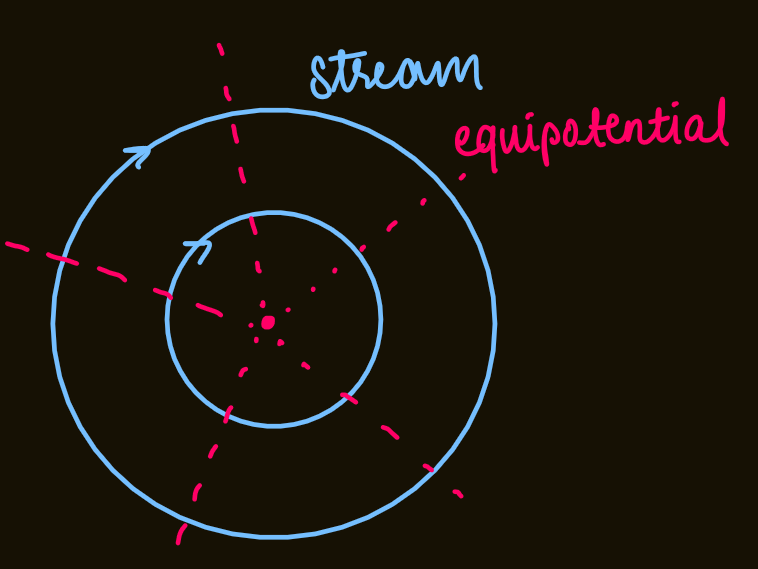
tornado/free vortex

this is a flow with circular paths around an axis
considering $\vec{u} = u_{θ} (r) \hat{θ}$
it is irrotational as $\vec{\nabla} \times \vec{u} = 0$

⟹ \frac{1}{r} \frac{\partial (r u_{θ})}{\partial r} = 0

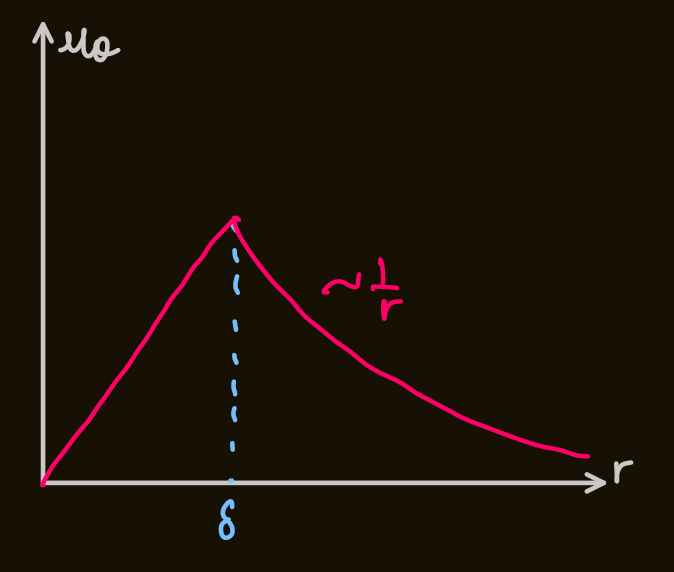
this means that $r u_{θ}$ must be constant
it is only possible for:

u_{θ} = \frac{K}{2 π} \frac{1}{r}

for $r \to 0$ , $u_{θ} \to \infty$ , which would be impossible
therefore, near $r = 0$ , viscosity must be accounted for
therefore the potential flow model works for $r > δ$

calculating the circulation around the axis:

\oint_{Γ} \vec{u} \cdot d \vec{l} = \int_{0}^{2 π} u_{θ} r d θ = \frac{K}{2 π} \int_{0}^{2 π} \frac{r}{r} d ρ = K

therefore, $K$ is the circulation around the axis
generally, $K \neq 0$ if $Γ$ is around $r = 0$ , ie. the axis
from kelvin's circulation theorem, $K = 0$ if $Γ$ is not around the axis
the potential:

u_{θ} (r) = \frac{1}{r} \frac{\partial ϕ}{\partial θ} ⟹ \frac{K}{2 π r} = \frac{1}{r} \frac{d ϕ}{d θ} ⟹ ϕ = \frac{K}{2 π} θ + c

the density is constant as it is incompressible
the pressure: at $r \to \infty$ , $\vec{u} \to 0$ , $p = p_{a t m}$
using the navier-stokes equation in euler form as it is inviscid, considering a stationary case, ie: $\partial_{t} = 0$
$g$ is also neglected

\begin{matrix} ρ [(\vec{u} \cdot \vec{\nabla}) \vec{u}]_{r} = - \frac{\partial p}{\partial r} \\ - ρ \frac{u_{θ}^{2}}{r} = - \frac{d p}{d r} \\ - \frac{ρ K^{2}}{4 π^{2}} \int \frac{1}{r^{3}} d r = - \int d p \\ ∴ p = - \frac{K^{2} ρ^{2}}{8 π r^{2}} \end{matrix}

as $p (r = \infty) = p_{a t m} :$

p = p_{a t m} - \frac{K^{2} ρ^{2}}{8 π r^{2}}

ie. $p$ decreases towards the tornado