PX285 - K2 - kelvin's circulation theorem

kelvin's circulation theorem

the circulation, $K$ , around a closed loop, $Γ$ , is moving with the fluid is constant for an inviscid flow

proof

\begin{aligned} \frac{d K}{d t} & = \frac{d}{d t} [\oint_{Γ} \vec{u} \cdot d \vec{l}] \\ = \underset{I_{1}}{\underset{⏟}{\oint_{Γ} \frac{d \vec{u}}{d t} \cdot d \vec{l}}} + \underset{I_{2}}{\underset{⏟}{\oint_{Γ} \vec{u} \cdot \frac{d}{d t} (d \vec{l})}} \end{aligned}

considering two nearby points on $Γ$

\begin{matrix} d \vec{l} = {\vec{r}}_{2} - {\vec{r}}_{1} \\ \frac{d}{d t} d \vec{l} = \frac{d \vec{r_{2}}}{d t} - \frac{d \vec{r_{2}}}{d t} = {\vec{u}}_{2} - {\vec{u}}_{1} = d \vec{u} \\ ∴ I_{2} = \oint_{Γ} \vec{u} \frac{d}{d t} (\vec{l}) = \oint_{Γ} \vec{u} \cdot d \vec{u} \\ = \oint_{Γ} d (\frac{u^{2}}{2}) = 0 \\ ∴ I_{2} = 0 \end{matrix}

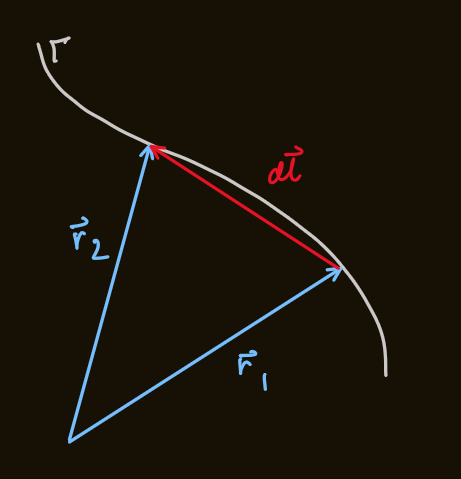
the integral vanishes because it is the integral of a perfect differential along a closed path (ie. starting point = end point)
for $I_{1}$ , using the navier-stokes equation:

\begin{matrix} \frac{d \vec{u}}{d t} = - \frac{1}{ρ} \vec{\nabla} p + g \vec{\nabla} z \\ ∴ \frac{d K}{d t} = \oint_{Γ} (- \frac{\vec{\nabla} p}{ρ} + g \vec{\nabla} z) \cdot d \vec{l} \end{matrix}

$\vec{\nabla} z = \vec{k}$ and:

\oint g (\vec{\nabla} z) \cdot d \vec{l} = 0

the integral around a closed loop for conservative fields is zero

∴ \frac{d K}{d t} = \oint - \frac{1}{ρ} \vec{\nabla} p \cdot d \vec{l}

incompressible

considering the incompressible limit: $\vec{\nabla} \cdot \vec{u} = 0$

\frac{d K}{d t} = \frac{1}{ρ} \oint_{Γ} (- \vec{\nabla} p) \cdot d \vec{l} = - \frac{1}{ρ} \oint_{Γ} d p = 0

therefore, $K$ is a constant, or, an invariant of fluid motion, and this proves the theorem

barotropic

for a barotropic fluid, $ρ = ρ (p)$ only
eg: adiabatic processes:

\frac{p}{ρ^{γ}} = constant ⟹ p \propto ρ^{γ}

eg: isothermal process: $γ = 1$
applying stokes' theorem and some vector identities:

\oint_{Γ} - \frac{1}{ρ} (\vec{\nabla} p) \cdot d \vec{l} = \iint_{S} [\vec{\nabla} \times (- \frac{\vec{\nabla} p}{ρ})] \cdot d \vec{S} = \iint_{S} \frac{1}{ρ^{2}} [\vec{\nabla} ρ \times \vec{\nabla} p] \cdot d \vec{S}

for a barotropic fluid, the density gradient is parallel to the pressure gradient:

\vec{\nabla} ρ = \frac{\partial ρ}{\partial p} \cdot \vec{\nabla} p

∴ \frac{d K}{d t} = \iint_{S} \frac{1}{ρ^{2}} \frac{\partial ρ}{\partial p} [\vec{\nabla} p \times \vec{\nabla} p] \cdot d \vec{S} = 0

therefore, the theorem is true for an inviscid fluid if it is either incompressible or barotropic