PX285 - J3 - water drain

considering water draining from a tank through a pipe at its base
$P_{a t m}$ applies at the water surface as well as the mouth of the pipe

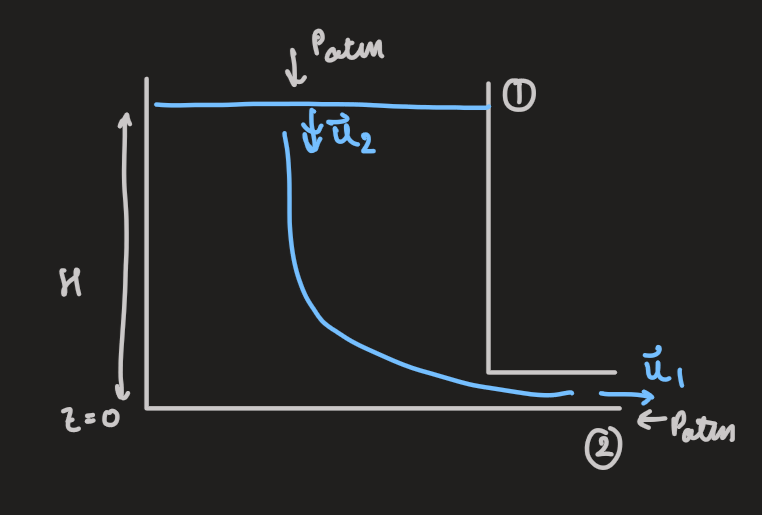
applying bernoulli's principle:

\begin{aligned} P_{a t m} + \frac{ρ u_{1}^{2}}{2} + ρ g H & = P_{a t m} + \frac{ρ u_{2}^{2}}{2} \\ ρ g H & = \frac{ρ}{2} (u_{2}^{2} - u_{1}^{2}) \end{aligned}

assuming the pipe is narrow, ie: $u_{2} ≫ u_{1} :$

u_{2} \approx \sqrt{2 g H}

this is the freefall speed
from conservation of energy:

\begin{matrix} m g H = \frac{1}{2} m v^{2} \\ v = \sqrt{2 g H} \end{matrix}

assuming the flow to be slow, ie. bernoulli's principle is applicable
the cross section of the tank, $A_{t}$ , and the cross section of the pipe, $A_{p}$ , such that $A_{t} ≫ A_{p}$
the initial volume of water:

V (t = 0) = A_{t} H (t = 0)

when it drains completely, $H = 0 :$

V (t_{d}) = A_{t} \times 0

the rate of change of the volume:

\frac{d V}{d t} = A_{t} \frac{d H}{d t} = - A_{p} u_{z} (H) = - A_{p} \sqrt{2 g H (t)}

solving the ODE by separation of variables:

A_{t} \int_{H (0)}^{0} \frac{d H}{H^{1 / 2}} = - A_{p} \sqrt{2 g} \int_{0}^{t_{d}} d t

∴ t_{d} = \frac{A_{t}}{A_{p}} \sqrt{\frac{2 H (0)}{g}}

here, the fluid speed remains constant regardless of the depth
but, it is known that the speed at the pipe, $u_{2}$ , is faster than at the surface, $u_{1}$
this leads to the conclusion that the speed goes from $u_{1}$ to $u_{2}$ instantaneously at the outflow entrance
this arises due to the assumptions that the fluid speed in the rank is zero, and the fluid is incompressible