PX285 - I5 - initial and boundary conditions

considering a rigid object in flow at the object's boundary, $u_{⊥} = 0$ , locally normal to the boundary
boundary conditions:
- 'rigid wall'
- 'no flux', ie. nothing can flow into a solid, and on the surface of a moving object in a fluid, $\vec{u}$ matches the velocity of the object's boundary
- 'no slip': $u_{∥} = 0 ⟹ \vec{u} = 0$ at the boundary
rederiving the reynold's number from the navier-stokes equation
considering flow over an obstacle

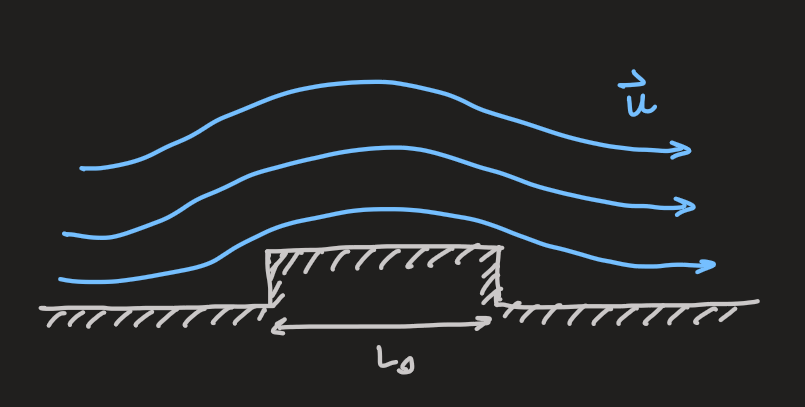
comparing the inertial and the viscous terms:

\begin{matrix} | ρ (\vec{u} \cdot \vec{\nabla}) \vec{u} | \sim \frac{ρ_{0} u_{0}^{2}}{L_{0}} \\ | μ \nabla^{2} \vec{u} | \sim \frac{μ u_{0}}{L_{0}^{2}} \end{matrix}

where, $\nabla \sim 1 / L_{0}$

the ratio of the inertial and the viscous terms:

\frac{ρ_{0} u^{2}}{L_{0}} \cdot \frac{L_{0}^{2}}{μ u_{0}} = \frac{ρ_{0} u_{0} L_{0}}{μ} = R e

so, reynold's number estimates the relative importance of the inertial and he viscous terms
if it is large, the flow is inviscid, $μ = 0$
if it is small, the inertial flow can be neglected, $ρ \frac{\partial \vec{u}}{\partial t} =$ force densities
eg: the pousselle flow:

0 = ρ \frac{\partial \vec{u}}{\partial t} = - \vec{\nabla} P + μ \nabla^{2} \vec{u} - \frac{\partial ρ}{\partial x} + μ \frac{\partial^{2} u_{x}}{\partial y^{2}}

since the navier-stokes equation is a second order PDE, there is a need for $u_{∥}$ , $u_{⊥}$ at boundaries
in the inviscid limit, terms with $μ \to 0$
this turns into a first order PDE - euler equation
only one boundary condition is needed, eg. for $u_{⊥}$

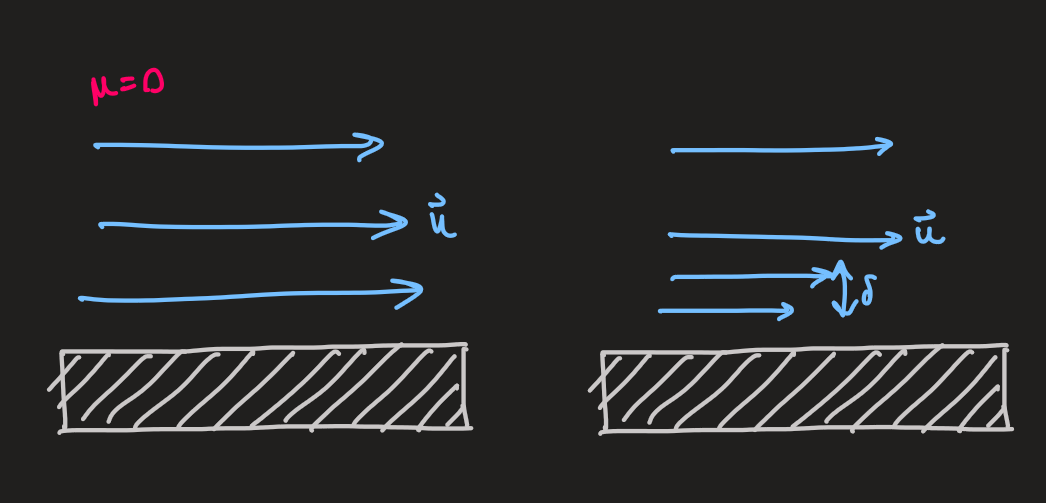
the velocity experiences a 'sharp' gradient near the boundary
euler and navier-stokes equations are similar except for a width, $δ$ , near the boundary - transition region
hence, the inertial and viscous terms:

\begin{matrix} | ρ (\vec{u} \cdot \vec{\nabla}) \vec{u} | \sim \frac{ρ_{0} u_{0}^{2}}{L_{0}} \\ | μ \nabla^{2} \vec{u} | \sim \frac{μ u_{0}}{δ^{2}} \end{matrix}

at the outer boundary of transition region:

\frac{ρ_{0} u_{0}^{2}}{L_{0}} \sim \frac{μ u_{0}}{δ^{2}}

\frac{δ}{L_{0}} \approx \sqrt{\frac{μ}{ρ_{0} u_{0} L_{0}}} = (R e)^{- 1 / 2}

for large reynolds number flows, thin layer near the boundary where viscosity cannot be ignored
this is called the boundary layer
outside this, $μ = 0$ will be an accurate model