PX285 - G9 - triatomic molecule

the euler-lagrange equation and modes

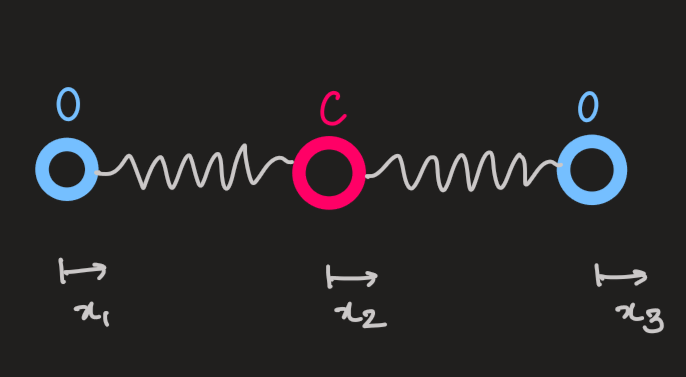
now, considering a carbon dioxide molecule (CO $_{2}$ )

\begin{matrix} T = \frac{1}{2} m_{O} {\dot{{\vec{x}}_{1}}}^{2} + \frac{1}{2} m_{C} {\dot{{\vec{x}}_{2}}}^{2} + \frac{1}{2} m_{O} {\dot{{\vec{x}}_{3}}}^{2} \\ V = \frac{1}{2} k (x_{2} - x_{1})^{2} + \frac{1}{2} k (x_{3} -) \end{matrix}

the inertia matrix:

M = (\begin{matrix} m_{O} & 0 & 0 \\ 0 & m_{C} & 0 \\ 0 & 0 & m_{O} \end{matrix})

the stiffness matrix:

K = (\begin{matrix} k & - k & 0 \\ - k & 2 k & - k \\ 0 & - k & k \end{matrix})

the euler-lagrange equation in matric form:

\begin{matrix} (1) & M \ddot{\vec{x}} = - K \vec{x} \end{matrix}

assuming $\vec{x} (t) = A \vec{X} e^{i ω t}$ , so, $\ddot{\vec{x}} = - ω^{2} \vec{x}$
substituting into equation $(1) :$

- ω^{2} M A \vec{X} e^{i ω t} = - A K \vec{X} e^{i ω t}

this should be equal for all time
for an arbitrary non-zero amplitude, $A :$

\begin{matrix} A e^{i ω t} [ω^{2} M \vec{X} - K \vec{X}] = \vec{0} \\ ⟹ (ω^{2} M - K) \vec{X} = \vec{0} \end{matrix}

considering the secular equation:

\begin{matrix} det (ω^{2} M - K) = 0 \\ | \begin{matrix} ω^{2} m_{O} - k & k & 0 \\ k & ω^{2} m_{C} - 2 k & k \\ 0 & k & ω^{2} m_{O} - k \end{matrix} | = 0 \\ ⟹ (ω^{2} m_{O} - k) ((ω^{2} m_{C} - 2 k) (ω^{2} m_{O} - k) - k^{2}) = 0 \\ and - k (k (ω^{2} m_{O} - k) - 0) = 0 \end{matrix}

this results in a cubic in $ω^{2}$ , so expect three roots with corresponding frequencies
from the first equation:

(m_{0} ω^{2} - k) ω^{2} [ω^{2} - \frac{k}{γ}] m_{O} m_{C} = 0

where, $γ = \frac{m_{O} m_{C}}{2 m_{O} + m_{C}}$

this gives three solutions:

\begin{aligned} ω^{(1)} & = \sqrt{\frac{k}{m_{O}}} \\ ω^{(2)} & = 0 \\ ω^{(3)} & = \sqrt{\frac{k}{γ}} \end{aligned}

the first mode

substituting it to equation $(1)$ will yield:

\begin{matrix} b = 0 \\ a = - c \end{matrix}

∴ {\vec{X}}^{(1)} = (\begin{matrix} a \\ b \\ c \end{matrix}) = a (\begin{matrix} 1 \\ 0 \\ - 1 \end{matrix})

the second mode

$ω^{(2)}$ represents translation
$M \ddot{\vec{x}} = 0$ is recovered for $\vec{x} (t) = A \vec{X} f (t)$ , with $f (t) = 1 + \frac{B}{A} t$
$- K \vec{X} = \vec{0} :$

(\begin{matrix} k & - k & 0 \\ - k & 2 k & - k \\ 0 & - k & k \end{matrix}) (\begin{matrix} 1 \\ a \\ b \end{matrix}) = \vec{0}

\begin{matrix} k (1 - a) = 0 & ⟹ & a = 1 \\ k (- 1 + 2 a - b) = 0 & ⟹ & b = 2 a - 1 = 1 \\ k (- a + b) = 0 & ⟹ & a = b \end{matrix}

∴ {\vec{X}}^{(2)} = (\begin{matrix} 1 \\ 1 \\ 1 \end{matrix})

the general solution:

\vec{x} (t) = (A^{(2)} + B^{(2)} t) (\begin{matrix} 1 \\ 1 \\ 1 \end{matrix}) t

the third mode

\1\n\2\n