PX285 - G8 - diatomic molecule

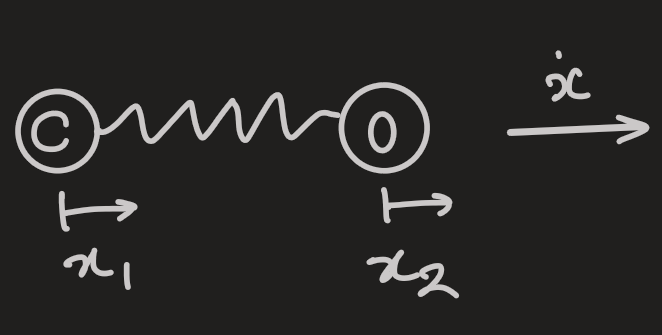
considering a diatomic molecule - carbon monoxide (CO)
the bond can be approximated as an ideal spring for small displacements

\begin{matrix} V = \frac{1}{2} k (x_{2} - x_{1})^{2} \\ T = \frac{1}{2} m_{C} {\dot{x}}_{1}^{2} + \frac{1}{2} m_{O} {\dot{x}}_{2}^{2} \end{matrix}

the inertia matrix

using the formula:

M_{i j} = \frac{\partial^{2} T}{\partial {\dot{x}}_{i} \partial {\dot{x}}_{j}}

the inertia matrix is:

M = (\begin{matrix} m_{C} & 0 \\ 0 & m_{O} \end{matrix})

the stiffness matrix

using the formula:

K_{i j} = \frac{\partial^{2} V}{\partial x_{i} \partial x_{j}}

the stiffness matrix is:

T = (\begin{matrix} k & - k \\ - k & k \end{matrix})

the euler-lagrange equation in matrix form

\begin{matrix} (1) & M \vec{\ddot{x}} = K \vec{x} \end{matrix}

the value of $\vec{x} = (\begin{matrix} x_{1} \\ x_{2} \end{matrix})$
guessing that there will be an oscillatory solution:

\vec{x} = A \vec{X} e^{i ω t}

substituting this into equation $(1) :$

\begin{matrix} - ω^{2} M \vec{X} = - K \vec{X} \\ (ω^{2} M - K) \vec{X} = \vec{0} \end{matrix}

the secular equation:

\begin{matrix} det (ω^{2} M - K) = 0 \\ | \begin{matrix} m_{C} ω^{2} - k & k \\ k & m_{O} ω^{2} - k \end{matrix} | = 0 \\ (m_{C} ω^{2} - k) (m_{O} ω^{2} - k) - k^{2} = 0 \\ m_{C} m_{O} (ω^{2})^{2} - k (m_{C} + m_{0}) ω^{2} = 0 \end{matrix}

\begin{matrix} either, & m_{C} m_{O} ω^{2} - k (m_{C} + m_{O}) = 0 & or, & ω^{2} = 0 \end{matrix}

the first mode

ω^{(1)} = \sqrt{k \frac{m_{C} + m_{O}}{m_{C} m_{O}}}

defining the reduced mass as:

μ = \frac{m_{C} m_{O}}{m_{C} + m_{O}}

ω^{(1)} = \sqrt{\frac{k}{μ}}

substituting this solution into equation $(1) :$

\begin{matrix} (M (ω^{(1)})^{2} - K) \vec{X} = \vec{0} \\ (\begin{matrix} m_{C} \frac{k}{μ} - k & k \\ k & m_{O} \frac{k}{μ} - k \end{matrix}) (\begin{matrix} a \\ b \end{matrix}) = \vec{0} \end{matrix}

this gives two equations:

\begin{matrix} (m_{C} \frac{k}{μ} - k) a + k b \\ \frac{a}{b} = \frac{k}{k - \frac{m_{C}}{μ}} = \dots = - \frac{m_{0}}{m_{C}} \\ ⟹ a = - m_{0}, and b = m_{C} \end{matrix}

the second mode

(ω^{(2)})^{2} = 0

this is a signature that is not an oscillating solution, but a translating one:

ω = 0 ⟹ τ = \frac{2 π}{ω} \to \infty

this can be understood as a translational mode

x (t) = (A + B t) (\begin{matrix} 1 \\ 1 \end{matrix})

where, $A$ is the position at $t = 0$ , $B$ is the velocity of translation, and the vector represents that both atoms are translating together

the masses moving together would imply that the spring like bond is never disturbed, ie. there are no external force
from newton's second law, the system should remain in its state of uniform motion