PX285 - G7 - example

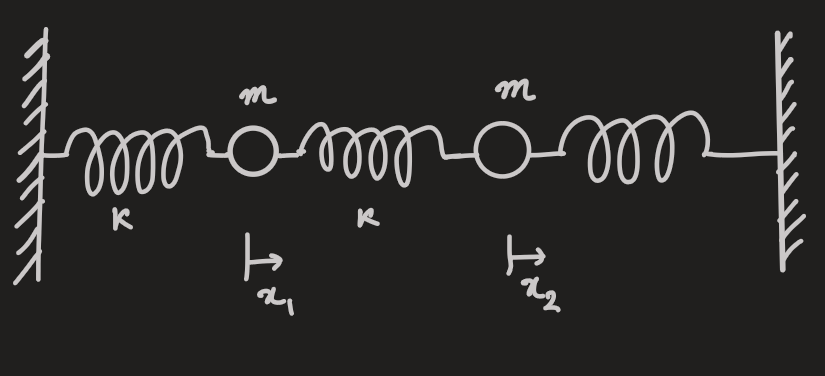
the inertia and stiffness matrices

the total kinetic energy:

T = \frac{1}{2} m {\dot{x}}_{1}^{2} + \frac{1}{2} m {\dot{x}}_{2}^{2}

the inertia matrix:

M = (\begin{matrix} \frac{\partial^{2} T}{\partial {\dot{x}}_{1}^{2}} & \frac{\partial^{2} T}{\partial {\dot{x}}_{1} \partial {\dot{x}}_{2}} \\ \frac{\partial^{2} T}{\partial {\dot{x}}_{2} \partial {\dot{x}}_{1}} & \frac{\partial^{2} T}{\partial {\dot{x}}_{2}^{2}} \end{matrix}) = (\begin{matrix} m & 0 \\ 0 & m \end{matrix})

the potential energy:

V = \frac{1}{2} k x_{1}^{2} + \frac{1}{2} k_{(} x_{2} - x_{1})^{2} + \frac{1}{2} (- x_{2})^{2}

the stiffness matrix:

K = (\begin{matrix} \frac{\partial^{2} V}{\partial x_{1}^{2}} & \frac{\partial^{2} V}{\partial x_{1} \partial x_{2}} \\ \frac{\partial^{2} V}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} V}{\partial x_{2}^{2}} \end{matrix}) = (\begin{matrix} 2 k & - k \\ - k & 2 k \end{matrix})

these can now be used to solve the vector euler-lagrange equation:

M \ddot{\vec{x}} = - K \vec{x}

the solutions are sinusoidal in time $(\sim \exp (i ω t))$ and satisfy the condition: $det (K - ω^{2} M) = 0$

| \begin{matrix} 2 k - ω^{2} m & - k \\ - k & 2 k - ω^{2} m \end{matrix} | = (2 k - ω^{2} m)^{2} - k^{2} = 0

\begin{matrix} 2 k - ω^{2} m = + k ⟹ ω^{(1)} = \sqrt{\frac{k}{m}} \\ 2 k - ω^{2} m = - k ⟹ ω^{(3)} = \sqrt{\frac{3 k}{m}} \end{matrix}

these are the first and second modes

first mode

B = K - ω^{(1)} M = (\begin{matrix} k & - k \\ - k & k \end{matrix})

hence,

(\begin{matrix} k & - k \\ - k & k \end{matrix}) {\vec{X}}^{(1)} = \vec{0}

$X^{(n)} = (\begin{matrix} a \\ b \end{matrix}) :$

\begin{aligned} k a - k b & = 0 \\ - k a + k b & = 0 \end{aligned}

these are two redundant solutions that give:

a = b

the scale is not known, but the amplitudes are arbitrary
thus the first mode is:

{\vec{x}}^{(1)} (t) = A^{(1)} (\begin{matrix} 1 \\ 1 \end{matrix}) \exp (i ω t)

second mode

B = K - ω^{(2)} M = (\begin{matrix} - k & - k \\ - k & - k \end{matrix})

hence,

(\begin{matrix} - k & - k \\ - k & - k \end{matrix}) {\vec{X}}^{(2)} = \vec{0}

$X^{(n)} = (\begin{matrix} a \\ b \end{matrix}) :$

\begin{aligned} - k a - k b & = 0 \\ - k a - k b & = 0 \end{aligned}

again, these are two redundant solutions that give:

a = - b

the scale is not known, but the amplitudes are arbitrary
thus the first mode is:

{\vec{x}}^{(2)} (t) = A^{(2)} (\begin{matrix} 1 \\ - 1 \end{matrix}) \exp (i ω t)

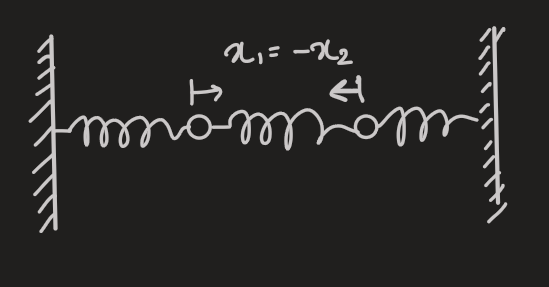
general solution

\vec{x} (t) = A^{(1)} (\begin{matrix} 1 \\ 1 \end{matrix}) \exp (i ω t) + A^{(2)} (\begin{matrix} 1 \\ - 1 \end{matrix}) \exp (i ω t)

considering the initial conditions: $x_{1} (t) = t$ , $x_{2} (t) = - t$ , and ${\dot{x}}_{1} = {\dot{x}}_{2} = 0 :$

\vec{x} (0) = A^{(1)} (\begin{matrix} 1 \\ 1 \end{matrix}) + A^{(2)} (\begin{matrix} 1 \\ - 1 \end{matrix})

the initial conditions are only satisfied by the second mode, so: $A^{(1)} = 0$ , and $A^{(} 2) = t$
considering the initial conditions: $x_{1} (0) = x_{2} (0) = 0$ , and ${\dot{x}}_{1} (0) = {\dot{x}}_{2} (0) = δ :$

\begin{matrix} \dot{\vec{x}} = i ω^{(1)} A^{(1)} (\begin{matrix} 1 \\ 1 \end{matrix}) \exp (i ω^{(1)} t) + i ω^{(2)} A^{(2)} (\begin{matrix} 1 \\ - 1 \end{matrix}) \exp (i ω^{(2)} t) \\ \dot{\vec{x}} (0) = i ω^{(1)} A^{(1)} (\begin{matrix} 1 \\ 1 \end{matrix}) + i ω^{(2)} A^{(2)} (\begin{matrix} 1 \\ - 1 \end{matrix}) \end{matrix}

this requires $A^{(2)} = 0$ and $i ω A^{(1)} = δ$

\begin{matrix} I m (i ω^{(1)} A^{(1)}) = δ, & I m (A^{(2)}) = 0, \\ R e (A^{(1)}) = 0, & R e (A^{(2)}) = 0 \end{matrix}

\vec{x} (0) = A^{(1)} (\begin{matrix} 1 \\ 1 \end{matrix}) + A^{(2)} (\begin{matrix} 1 \\ - 1 \end{matrix}) = 0

∴ \vec{x} (t) = - \frac{i δ}{ω^{(1)}} (\begin{matrix} 1 \\ 1 \end{matrix}) \exp (i ω^{(1)}) = \frac{δ}{ω^{(1)}} (\begin{matrix} 1 \\ 1 \end{matrix}) \exp (i ω^{(1)} t + \frac{3}{2} π)