PX285 - G5 - non-diagonal inertia matrix

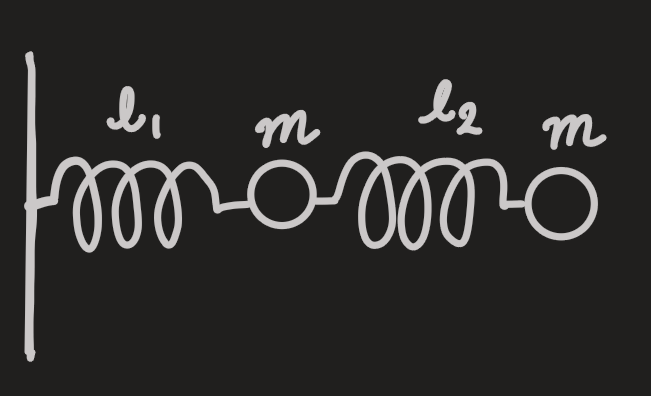
the velocity of the first mass is ${\dot{l}}_{1}$ , and of the second mass is ${\dot{l}}_{1} + {\dot{l}}_{2}$
the kinetic energy of the system:

T = \frac{1}{2} m {\dot{l}}_{1}^{2} + \frac{1}{2} m ({\dot{l}}_{1} + {\dot{l}}_{2})^{2} = m {\dot{l}}_{1}^{2} + \frac{1}{2} m {\dot{l}}_{2}^{2} + \frac{1}{2} m {\dot{l}}_{1} {\dot{l}}_{2}

${\dot{l}}_{1} {\dot{l}}_{2}$ is an off-diagonal term
the inertia matrix:

M = (\begin{matrix} \frac{m}{2} & \frac{m}{2} \\ \frac{m}{2} & m \end{matrix})

the generalized force:

F_{k} = \frac{\partial L}{\partial x_{k}} = - \frac{\partial V}{\partial x_{k}}

normal modes represent small displacements from the equilibrium when response is linear
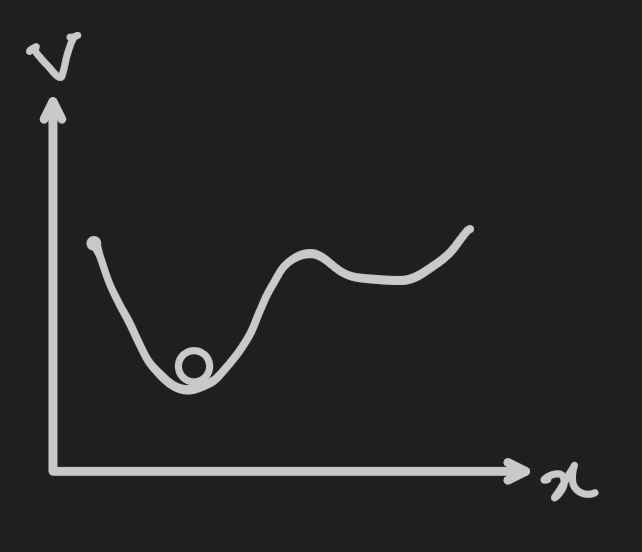
considering the case where the displacements are a small distance from an equilibrium point
equilibrium is defined to be when there is no force, or the potential is at the minimum:

F = - \frac{d V}{d x} = 0

at equilibrium in more than one dimension, all components of the force must vanish:

F_{i} = - \frac{\partial V}{\partial x_{i}} = 0 \forall i

a change of variables (shift of the coordinate axes)can be made to engineer the equilibrium point of interest to be at $x = 0$
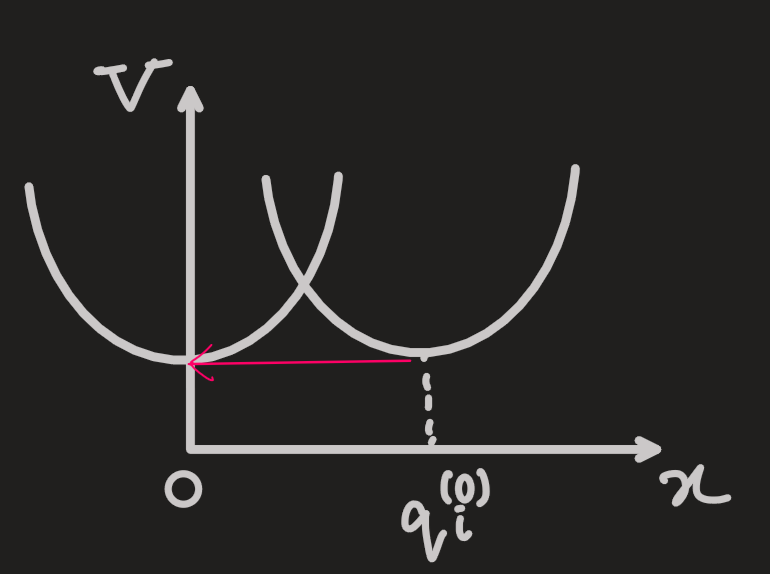
potential might have a minimum at $q_{i} = q_{i}^{(0)} \neq 0$
so, a new coordinate can be defined such that: $x_{i} = q_{i} - q_{i}^{(0)}$
this makes calculations convenient
the potential: $V (x_{1}, x_{2}, \dots) = V (\vec{x})$
taylor expansion about the equilibrium:

\begin{aligned} V (\vec{x}) & = V (0) + \sum_{i} \underset{= 0}{\underset{⏟}{\frac{\partial V}{\partial x_{i}} |_{\vec{x} = 0}}} x_{i} + \frac{1}{2} \sum_{i} \sum_{j} \frac{\partial^{2} V}{\partial x_{i} x_{j}} |_{\vec{x} = 0} + \dots \\ = V (0) + \frac{1}{2} \sum_{i} \sum_{j} \frac{\partial^{2} V}{\partial x_{i} x_{j}} |_{\vec{x} = 0} + \dots \end{aligned}

writing the second derivative as the stiffness matrix, $K_{i j}$

F_{k} = \frac{\partial L}{\partial x_{k}} = - \frac{\partial V}{\partial x_{k}}

where, $F_{k}$ is the $k^{t h}$ element of $\vec{F}$

\begin{aligned} F_{k} & \approx - \frac{\partial V}{\partial x_{k}} = - \frac{\partial}{\partial x_{k}} [V (0) + \frac{1}{2} \sum_{i j} K_{i j} x_{i} x_{j}] \\ = - \frac{1}{2} \sum_{i j} K_{i j} [\frac{\partial x_{i}}{\partial x_{j}} x_{k} + x_{i} \frac{\partial x_{j}}{\partial x_{k}}] \\ = - \frac{1}{2} \sum_{i j} K_{i j} [δ_{i k} x_{j} + x_{i} δ_{j k}] \\ = - \frac{1}{2} [\sum_{j} K_{k j} x_{j} + \sum_{i} K_{i k} x_{i}] \\ ∴ F_{k} & = - \sum_{i k} K_{i k} x_{i} \end{aligned}

⟹ \frac{d}{d t} \sum_{i} M_{i k} {\dot{x}}_{i} = \sum_{i} M_{i k} {\ddot{x}}_{i} = - \sum_{i} K_{i k} x_{i}

this can be written as:

M \ddot{\vec{x}} = - k \vec{x}

where $M$ is the inertia matrix, and $K$ is the stiffness matrix

\begin{array}{r} M_{i j} = \frac{\partial^{2} T}{\partial {\dot{x}}_{i} \partial {\dot{x}}_{j}} \\ K_{i j} = \frac{\partial^{2} V}{\partial x_{i} \partial x_{j}} \end{array}