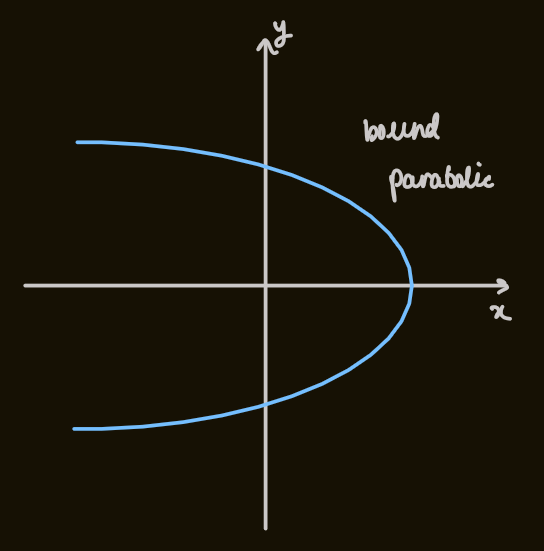
PX285 - F5 - central forces - particle approaching the sun

determining the lagrangian

considering the position vector of the particle in polar coordinates:

\vec{r} (t) = r (t) (\begin{matrix} \cos θ (t) \\ \sin θ (t) \end{matrix})

the velocity:

\vec{v} = \dot{r} (\begin{matrix} \cos θ (t) \\ \sin θ (t) \end{matrix}) + r \dot{θ} (\begin{matrix} - \sin θ (t) \\ \cos θ (t) \end{matrix}) = \dot{r} \hat{r} + r \dot{θ} \hat{θ}

the square of the velocity:

v^{2} = \vec{v} \cdot \vec{v} = (\dot{r} \hat{r} + r \dot{θ} \hat{θ}) \cdot (\dot{r} \hat{r} + r \dot{θ} \hat{θ}) = {\dot{r}}^{2} + (r \dot{θ})^{2}

the kinetic energy:

T = \frac{1}{2} m ({\dot{r}}^{2} + (r \dot{θ})^{2})

and the potential energy:

V = V (r)

therefore, the lagrangian is:

\begin{matrix} (1) & L = \frac{1}{2} m ({\dot{r}}^{2} + (r \dot{θ})^{2}) - V (r) \end{matrix}

formulating the euler-lagrange equations

the components of the canonical momentum:

\begin{aligned} (2) & \frac{\partial L}{\partial \dot{r}} = p_{r} & = m \dot{r} \\ (3) & \frac{\partial L}{\partial \dot{θ}} = p_{θ} & = m r^{2} \dot{θ} \end{aligned}

note: $p_{θ}$ does not have the dimensions of canonical momentum, it is the angular momentum
the time derivatives:

\begin{aligned} (4) & \frac{\partial L}{\partial r} & = {\dot{p}}_{r} = m r {\dot{θ}}^{2} - \frac{\partial V}{\partial r} \\ (5) & \frac{\partial L}{\partial θ} & = {\dot{p}}_{θ} = 0 \end{aligned}

the angular momentum, $p_{θ}$ , is a conserved quantity, and it arises from the rotational invariance of the system
from $(3) : \dot{θ} = \frac{p_{θ}}{m r^{2}}$
from $(2)$ and $(4) :$

\begin{aligned} \frac{d}{d t} (m \dot{r}) & = m r {\dot{θ}}^{2} - \frac{\partial V}{\partial r} \\ (6) & m \ddot{r} & = \frac{p_{θ}^{2}}{m r^{3}} - \frac{\partial V}{\partial r} = - \frac{\partial V_{e f f}}{\partial r} \end{aligned}

the effective potential:

V_{e f f} = V + \frac{1}{2} \frac{p_{θ}^{2}}{m r^{2}}

equation $(6)$ can be solved for $r (t)$

the energy of the system

considering the energy:

\begin{aligned} H = T + V & = \frac{1}{2} m ({\dot{r}}^{2} + (r \dot{θ})^{2}) + V (r) \\ = \frac{1}{2} m ({\dot{r}}^{2} + \frac{p_{θ}^{2}}{m^{2} r^{2}}) + V (r) \\ (7) & ∴ H (p_{r}, p_{θ}, r, θ) & = \frac{1}{2 m} p_{r}^{2} + \frac{1}{2 m r^{2}} p_{θ}^{2} + V (r) = E \end{aligned}

rearranging for $p_{r} :$

\begin{matrix} p_{r} = \sqrt{(E - V (r) - \frac{1}{2 m r^{2}} p_{θ}^{2}) 2 m} \\ (8) & ⟹ p_{r} = m \dot{r} = \sqrt{2 m (E - V_{e f f} (r))} \end{matrix}

the values of $r$ that are the roots of $(E - V_{e f f} (r)) = 0$ are points above $p_{r} = 0$

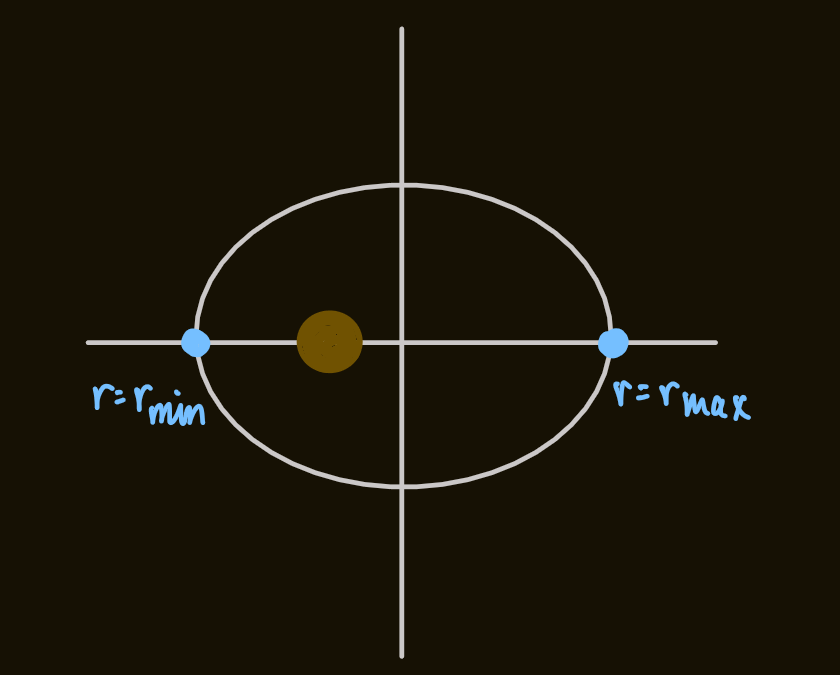
determining the trajectory

from equation $(3) :$

\begin{aligned} \frac{d θ}{d t} & = \frac{p_{θ}}{m r (t)^{2}} \\ \int d θ & = \int^{t} \frac{p_{θ}}{m r (t^{'})^{2}} d t^{'} \\ (9) & θ - θ_{0} & = \int_{0}^{t} \frac{p_{θ}}{m r (t)^{2}} d t \end{aligned}

from equation $(6) :$

m \ddot{r} = \frac{p_{θ}^{2}}{m r^{3}} - \frac{\partial V}{\partial r}

to solve this equation:
[1] adopting a parametric approach: $t \to θ$ , equivalently, changing the variables from $t$ to $θ$
[2] dealing with the inverse of $r$

[1] parameterization

\frac{d}{d t} = \frac{d θ}{d t} \frac{d}{d θ} = \frac{p_{θ}}{m r^{2}} \frac{d}{d θ}

thinking of $r (t)$ as $r (θ)$ , and from equation $(6) :$

m \frac{d^{2}}{d t^{2}} r (t) = m (\frac{p_{θ}}{m r^{2}} \frac{d}{d θ}) (\frac{p_{θ}}{m r^{2}} \frac{d}{d θ}) r (θ) = \frac{p_{θ}^{2}}{m r^{3}} - \frac{\partial V}{\partial r}

defining: $r^{'} = \frac{d r}{d θ}$ , $r^{″} = \frac{d^{2} r}{d θ^{2}} :$

\begin{aligned} \frac{p_{θ}^{2}}{m r^{3}} - \frac{\partial V}{\partial r} & = \frac{p_{θ}}{r^{2}} \frac{d}{d θ} (\frac{p_{θ}}{m r^{2}} r^{'}) \\ = \frac{p_{θ}}{r^{2}} [\frac{p_{θ}}{m r^{2}} r^{″} - 2 \frac{p_{θ}}{m r^{3}} (r^{'})^{2}] \\ (10) & \frac{p_{θ}^{2}}{m r^{3}} - \frac{\partial V}{\partial r} & = \frac{p_{θ}^{2}}{m r^{2}} [\frac{r^{″}}{r^{2}} - \frac{2 r^{' 2}}{r^{3}}] \end{aligned}

[2] considering the inverse

defining $u$ as the inverse of $r :$

\begin{matrix} u (θ) = \frac{1}{r (θ)} \\ u^{'} = \frac{d}{d θ} (\frac{1}{r}) = - \frac{r^{'}}{r^{2}} \\ u^{″} = \frac{d}{d θ} (- \frac{r^{'}}{r^{2}}) = - \frac{r^{″}}{r^{2}} + 2 \frac{(r^{'})^{2}}{r^{3}} \end{matrix}

equation $(10)$ can be written as:

\begin{matrix} (11) & \frac{p_{θ}^{2} u^{3}}{m} - \frac{\partial V}{\partial r} = \frac{p_{θ}^{2} u^{2}}{m} [- u^{″}] \end{matrix}

assuming $V (r) = - \frac{α}{r} :$

\frac{\partial V}{\partial r} = \frac{α}{r^{2}} = α u^{2}

using this in equation $(11) :$

\begin{aligned} \frac{p_{θ}^{2}}{m} u^{3} - α u^{2} & = - \frac{p_{θ}^{2}}{m} u^{2} u^{″} \\ - u + \frac{α m}{p_{θ}^{2}} & = u^{″} \\ u^{″} + u & = \frac{α m}{p_{θ}^{2}} = c o n s t a n t \end{aligned}

this is a second-order inhomogeneous differential equation

solving the second-order inhomogeneous differential equation

\begin{matrix} (12) & u^{″} + u = \frac{α m}{p_{θ}^{2}} \end{matrix}

considering the homogeneous part:

u^{″} + u = 0

which looks like SHM with $ω = 1$
the solutions of the complementary function will be:

u_{C F} = ϵ \cos (θ - θ_{0}) = A \cos θ + B \sin θ

the particular integral:

u_{P I} = \frac{α m}{p_{θ}^{2}}

the full solution:

\begin{matrix} (13) & u = u_{C F} + u_{P I} = ϵ \cos (θ - θ_{0}) + \frac{α m}{p_{θ}^{2}} \end{matrix}

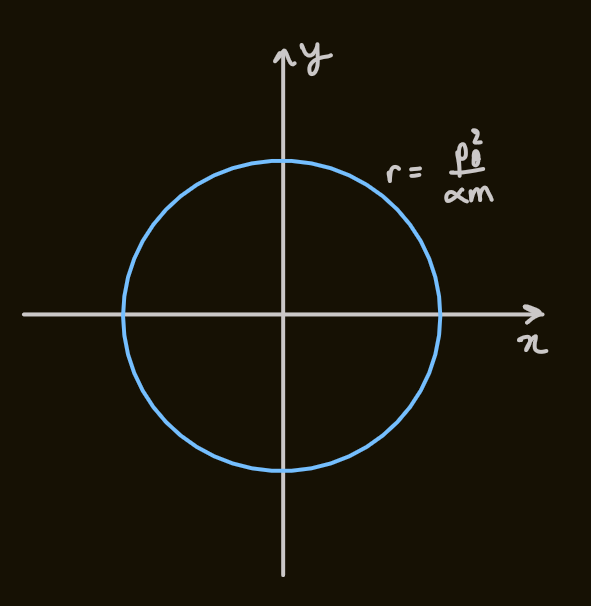
case 1

\begin{aligned} ϵ & = 0 \\ u & = \frac{α m}{p_{θ}^{2}} \\ ⟹ r & = \frac{p_{θ}^{2}}{α m} \end{aligned}

this is a trivial solution, which is circular orbit of constant radius, the direction given by the sign of $p_{θ}$

case 2

0 < ϵ < \frac{m α}{p_{θ}^{2}}

$u > 0$ because $ϵ < \frac{m α}{p_{θ}^{2}}$
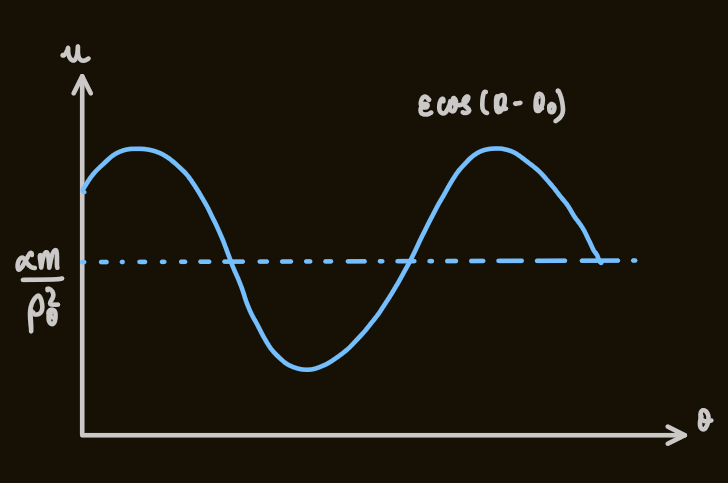
for unbound orbits, $r \to \infty : u \to 0$ , so this orbit is bound

\begin{aligned} u_{m a x} = ϵ + \frac{m α}{p_{θ}^{2}} & ⟹ r_{m i n} = \frac{1}{ϵ + \frac{m α}{p_{θ}^{2}}} \\ u_{m a x} = - ϵ + \frac{m α}{p_{θ}^{2}} & ⟹ r_{m i n} = \frac{1}{- ϵ + \frac{m α}{p_{θ}^{2}}} \end{aligned}

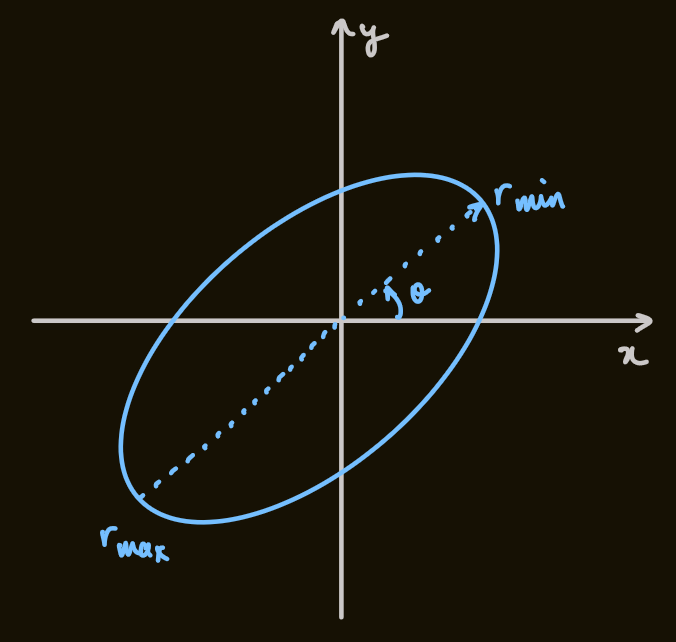
case 3

for

ϵ > \frac{m α}{p_{θ}^{2}}

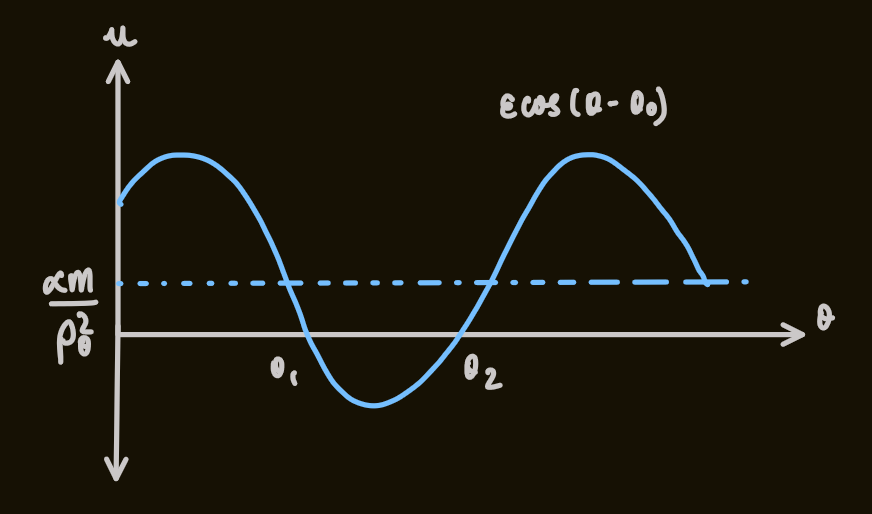
$u \to 0$ and $r \to \infty$ at two special angles: $θ_{1}, θ_{2}$
therefore, this is an unbound orbit, or a 'scattering' event, and the particle follows a hyperbolic orbit

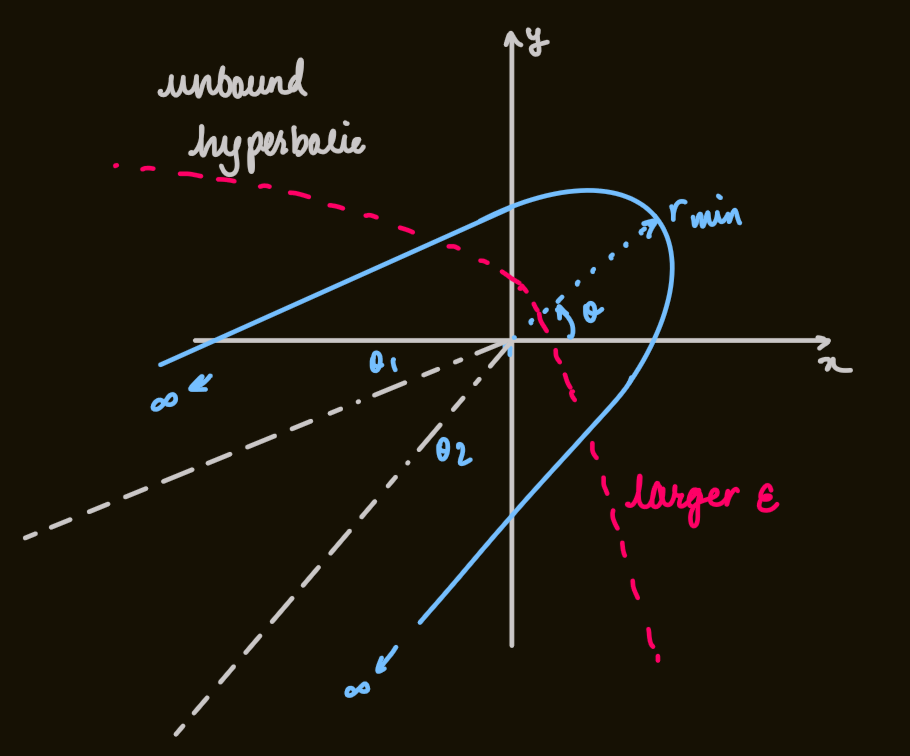
case 4

ϵ = \frac{m α}{p_{θ}^{2}}

the particle follows a bound parabolic orbit