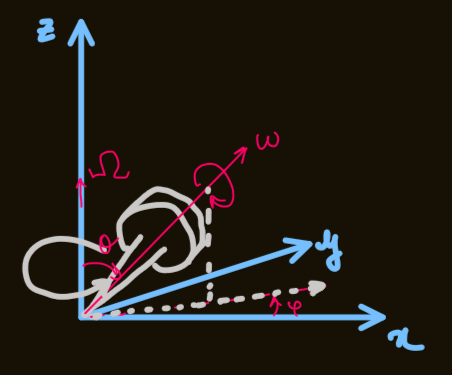
PX285 - F4 - gyroscope

considering a spinning top that can rotate on a fixed point
it has three rotational degrees of freedom: $θ$ , $α$ , and $ϕ$ ; but no translational degrees of freedom

reminder: for a uniform rod of length, $l$ , spinning about its centre of mass with an angular frequency, $ω$ , the kinetic energy is given by:

T = \frac{1}{2} I ω^{2}

where, $I = m l^{2}$ is the moment of inertia

the gyroscope has two moments of inertia, $I$ and $J$
the normal is the top symmetry axis
if the top is spinning at at angle to the normal, the moment of inertia is $I$
if it is spinning about the normal, then it is $J$

determining the lagrangian

potential energy

suppose $l$ is the distance from the base to the centre of mass of the top, and $θ$ is the angle with the normal
the potential energy: $$V = mgl\cos\theta$$

kinetic energy

the axes of rotation for top are represented by:
${\hat{e}}_{θ} ⊥$ plane of rotation, due to 'wobble'
${\hat{e}}_{ϕ} \sim \hat{z}$ , due to rotation about $z$ -axis
${\hat{e}}_{α} \sim \hat{r}$ , due to spin
these are not orthogonal

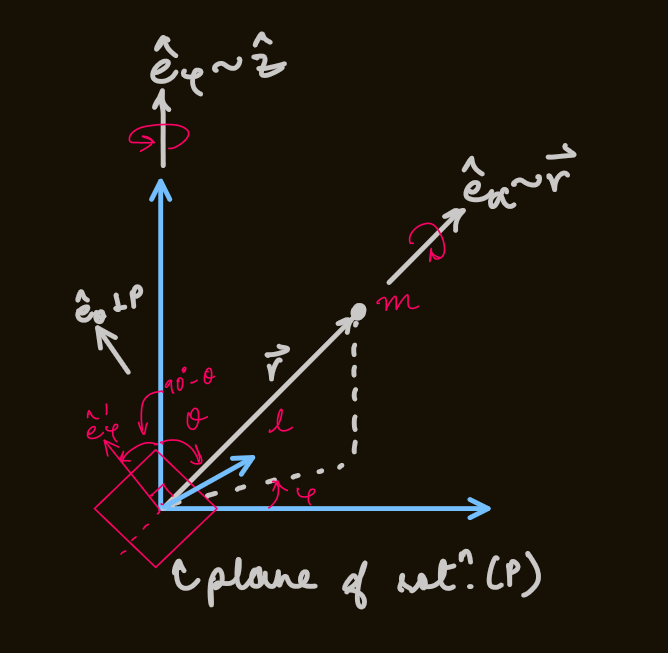
defining another unit vector, ${\hat{e}}_{ϕ}^{'}$ , such that ${\hat{e}}_{ϕ}^{'} ⊥ {\hat{e}}_{θ}$ and ${\hat{e}}_{α}$
therefore, $ϕ$ rotation is represented by: $\dot{ϕ} {\hat{e}}_{ϕ}$
taking its projection in the basis ${\hat{e}}_{ϕ} : \dot{ϕ} \sin θ {\hat{e}}_{ϕ}^{'}$

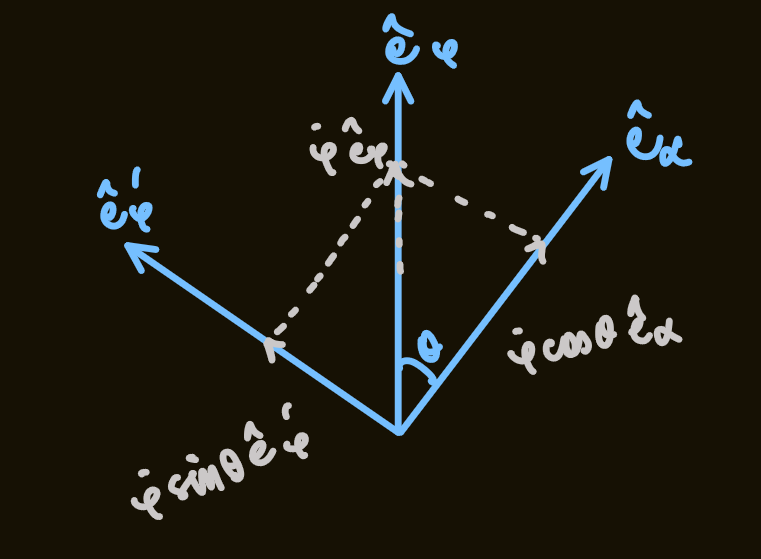
the spin frequency: $\dot{ω} = \dot{α} + \dot{ϕ} \cos θ$ about ${\hat{e}}_{α}$
the theta rotation is represented by: $\dot{θ} {\hat{e}}_{θ}$
therefore the three rotations are:

\begin{matrix} \dot{ϕ} \sin θ {\hat{e}}_{ϕ}^{'}, & (\dot{α} + \dot{ϕ} \cos θ) {\hat{e}}_{α} & \dot{θ} {\hat{e}}_{θ} \end{matrix}

hence, the kinetic energy is given by:

T = \frac{1}{2} I {\dot{θ}}^{2} + \frac{1}{2} I (\dot{ϕ} \sin θ)^{2} + \frac{1}{2} J (\dot{α} + \dot{ϕ} \cos θ)^{2}

where, $J$ is the moment of inertia about the axis of the top, and $I$ is that about the

the lagrangian

L = T - V = \frac{1}{2} I {\dot{θ}}^{2} + \frac{1}{2} I (\dot{ϕ} \sin θ)^{2} + \frac{1}{2} J (\dot{α} + \dot{ϕ} \cos θ)^{2} - m g l \cos θ

the euler-lagrange equation

the euler-lagrange equation:

\frac{\partial L}{\partial q_{i}} = \frac{d}{d t} \frac{\partial L}{\partial {\dot{q}}_{i}}

there will be three equations:
$q_{1} = θ$
$q_{2} = ϕ$
$q_{3} = α$
there will two rotational symmetries as $L$ does not depend on $ϕ$ or $α$
looking at $ϕ$ and $α$ equations first, anticipating the emergence of two conserved momenta:

\begin{matrix} \frac{\partial L}{\partial ϕ} = 0 = \frac{d}{d t} p_{ϕ} \\ p_{ϕ} = \frac{\partial L}{\partial \dot{ϕ}} = I \sin^{2} θ + J \cos θ (\dot{α} + \dot{ϕ} \cos θ) = c o n s t a n t \end{matrix}

\begin{matrix} \frac{\partial L}{\partial α} = 0 = \frac{d}{d t} p_{α} \\ p_{α} = \frac{\partial L}{\partial \dot{α}} = J (\dot{α} + \dot{ϕ} \cos θ) = c o n s t a n t \end{matrix}

\begin{matrix} (1) & ⟹ p_{ϕ} = I \sin^{2} θ \dot{ϕ} + \cos θ p_{α} = c o n s t a n t \end{matrix}

considering the $θ$ equation:

\frac{\partial L}{\partial θ} = I \sin θ \cos θ {\dot{ϕ}}^{2} - J \dot{ϕ} \sin θ (\dot{α} + \dot{ϕ} \cos θ) + m g l \sin θ

\frac{d}{d t} \frac{\partial L}{\partial \dot{θ}} = \frac{d}{d t} I \dot{θ} = I \ddot{θ}

\begin{aligned} I \ddot{θ} & = I \sin θ \cos θ {\dot{ϕ}}^{2} - J \dot{ϕ} \sin θ (\dot{α} + \dot{ϕ} \cos θ) + m g l \sin θ \\ = I \sin θ \cos θ {\dot{ϕ}}^{2} - \dot{ϕ} \sin θ p_{α} + m g l \sin θ \end{aligned}

from equation $(1) :$

\dot{ϕ} = \frac{p_{ϕ} - c o s θ p_{α}}{I \sin^{2} θ}

\begin{aligned} I \ddot{θ} & = I \sin θ \cos θ {(\frac{p_{ϕ} - c o s θ p_{α}}{I \sin^{2} θ})}^{2} \\ - p_{α} \sin θ (\frac{p_{ϕ} - c o s θ p_{α}}{I \sin^{2} θ}) + m g l \sin θ \\ = F (θ) \end{aligned}

this is a second order ODE that can be solved numerically