PX285 - F3b - pendulum
- considering a simple pendulum of length,
, and is the angle between the pendulum and the equilibrium position at a given time - writing down the lagrangian,
, and using it to calculate the hamiltonian, and identifying the momentum:
- note: here,
because this is the angular momentum - the definition of
from first principles:
- substituting for
- substituting using
- using hamilton's equations:
- if
- on phase plane:
- deriving the equations of motion:
where,
- for
- this is SHM with solutions:
- defining
as:
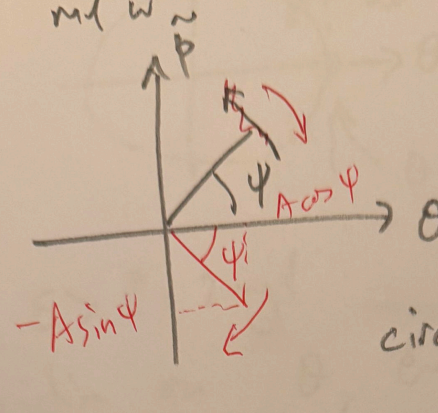
- a circular trajectory on the
plane with clockwise rotation - an elliptical trajectory on the
plane - the slope:
- the slope is negative
- if pendulum oscillates back and forth:
, , - if
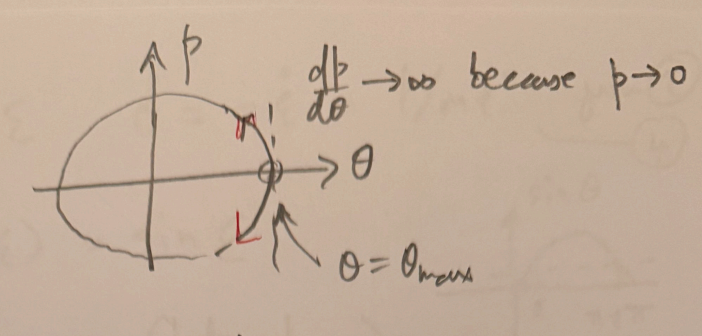
- if
no restriction on ,
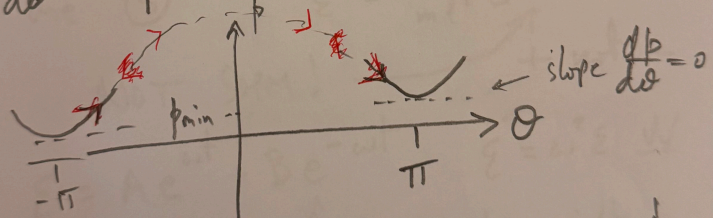
- if
, the pendulum can come to rest at - let,
- in the late stages,
- note: this is not SHM as there is a
, not - the solution:
- the first term is diverging from upright, while the second is converging to it
- here,
is getting smaller:
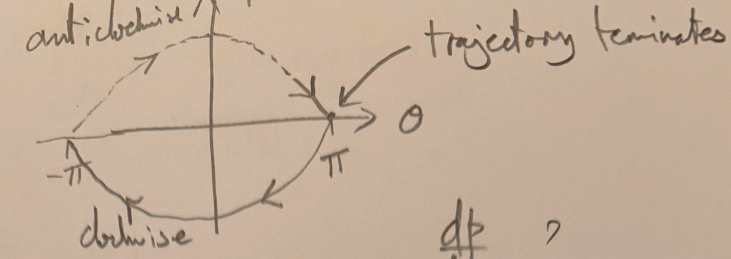
- seeking a expression for
- the gradient is a non-zero negative constant
disconnected trajectories
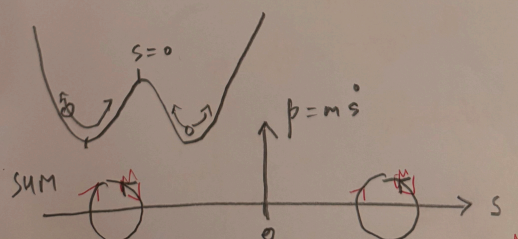
-
not all states of a given energy are necessarily accessible, this is called breaking of ergodicity
-
ergodic systems explore all sates consistent with energy conservation
-
considering a rollercoaster in a 'mexican hat' potential, where,
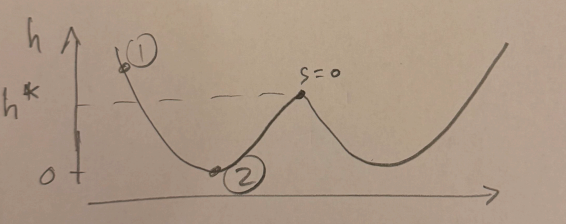
-
for
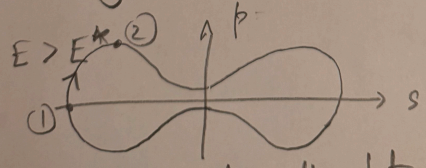
-
this is ergodic as it can explore all states consistent with energy,