PX284 - T3b - spherical surface using intersecting cords theorem

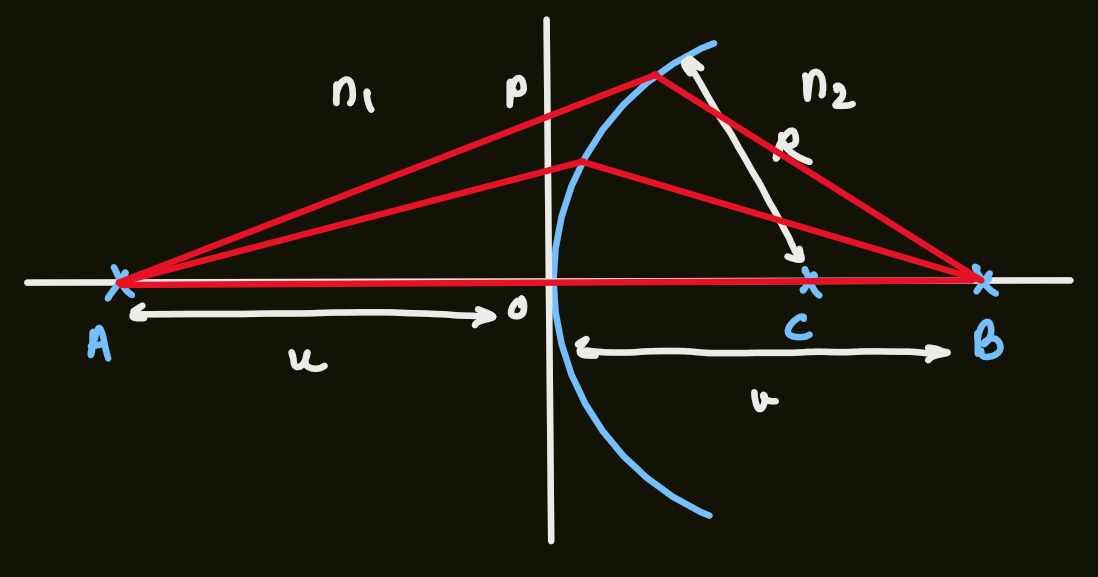
considering a spherical surface using 'real is positive' convention ( $u$ and $v > 0$ )
the optical path length $A P B :$

τ = n_{1} ((u + x)^{2} + y^{2})^{1 / 2} + n_{2} ((v - x)^{2} + y^{2})^{1 / 2}

intersecting cord theorem

when any two cords on a circle cross, the products of the length of the two pieces of each cord are equal

\begin{matrix} y^{2} = (2 R - x) x ⟹ x^{2} + y^{2} = 2 R x \\ ⟹ τ (x) = n_{1} \sqrt{u^{2} + 2 (R + u) x} + n_{2} \sqrt{v^{2} + (R - v) x} \end{matrix}

from fermat's principle:

\frac{d τ}{d x} = 0 = \frac{n_{1} (R + u)}{\sqrt{u^{2} + 2 (R + u) x}} + \frac{n_{2} (R - u)}{\sqrt{v^{2} + (R - v) x}}

limiting to 'paraxial rays', where the rays lie at small angles to the axis, so $x$ is small, AKA gaussian optics:

\frac{n_{1} (R + u)}{u} + \frac{n_{2} (R - u)}{v} = 0

∴ \frac{n_{1}}{u} + \frac{n_{2}}{v} = \frac{n_{2} - n_{1}}{R}

if the spherical surface curved the other way, $x \to - x :$

∴ \frac{n_{1}}{u} + \frac{n_{2}}{v} = - \frac{n_{2} - n_{1}}{R}

this is equivalent to setting $1 / R \to - 1 / R$ , referred to as 'negative radius of curvature'