PX284 - E3 - harmonic oscillator in 1D

considering a harmonic oscillator in 1D, the energy of states is:

E_{n} = (n + \frac{1}{2}) ℏ ω

the partition function:

\begin{aligned} Z & = \sum_{n} \exp (- β (n + \frac{1}{2}) ℏ ω) \\ = \exp (- \frac{β ℏ ω}{2}) \sum_{n} \exp (- β ℏ ω n) \end{aligned}

the above sum looks like a geometric series:

a \sum_{n}^{\infty} r^{n} = \frac{a}{1 - r}

with $a = \exp (- β ℏ ω / 2)$ , and $r - \exp (- β ℏ ω)$

therefore, it can be rewritten as:

\begin{aligned} Z & = \frac{\exp (- β ℏ ω / 2)}{1 - \exp (- β ℏ ω)} \\ \ln Z & = - \frac{β ℏ ω}{2} - \ln (1 - \exp (- β ℏ ω)) \end{aligned}

thus, the internal energy:

U = - \frac{d \ln Z}{d β} = ℏ ω [\frac{1}{2} + \frac{1}{\exp (β ℏ ω) - 1}]

the heat capacity:

C_{V} = {(\frac{\partial U}{\partial T})}_{V} = k_{B} (β ℏ ω)^{2} \frac{\exp (β ℏ ω)}{(\exp (β ℏ ω) - 1)^{2}}

at very high temperatures, $β ℏ ω ≪ 1 :$

⟹ \exp (β ℏ ω) \approx 1 + β ℏ ω

C_{V} \approx k_{B} {(\frac{β ℏ ω}{β ℏ ω})}^{2} = k_{B}

this is in keeping with the equipartition theorem

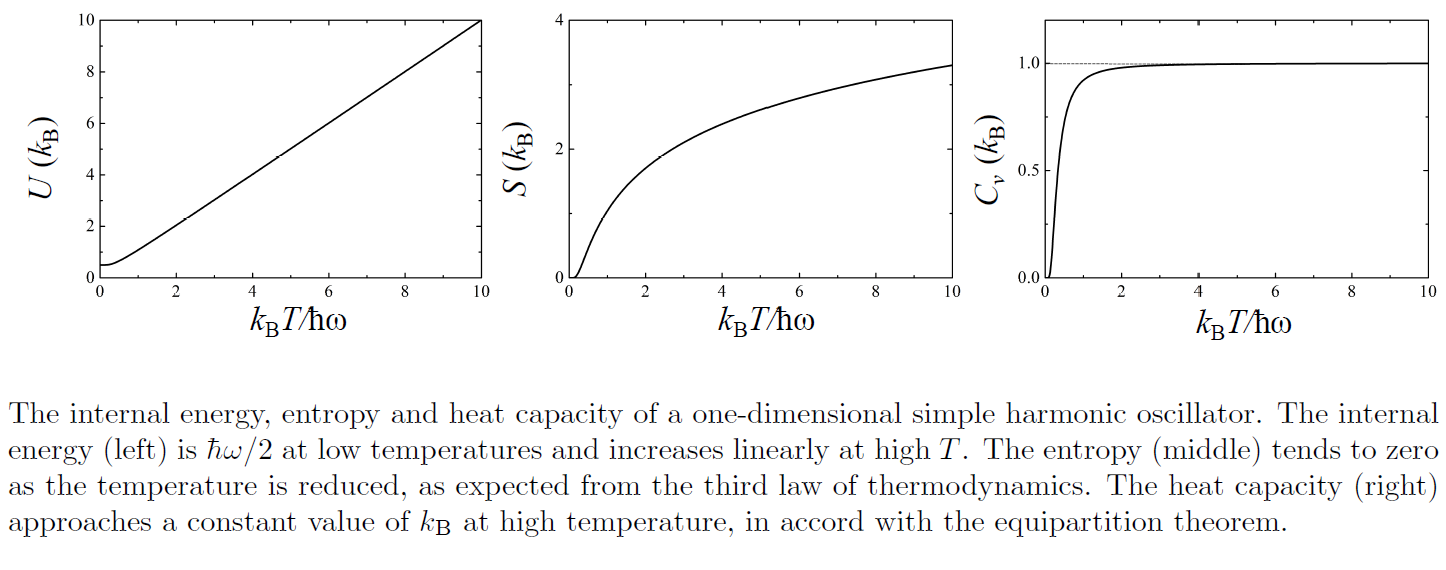
image: P. Goddard, lecture notes