PX282 - K2a - interiors of gas giants

the radius vs mass can be calculated for a given composition by assuming hydrostatic equilibrium
balancing gravity with pressure gradient:

\frac{d P}{d r} = - \frac{G M_{r} ρ (r)}{r^{2}}

where, $M_{r}$ is the mass enclosed within radius, r

to solve for $ρ (r)$ , $P (ρ)$ is needed, so the equation of state is needed
this can be very complex and difficult to measure at high pressures
but for H and He, it can be assumed that:

P ≃ K ρ^{2}

where, $K$ is a constant, empirically obtained to be $2.7 \times 10^{5}$ N m $^{4}$ kg $^{- 2}$

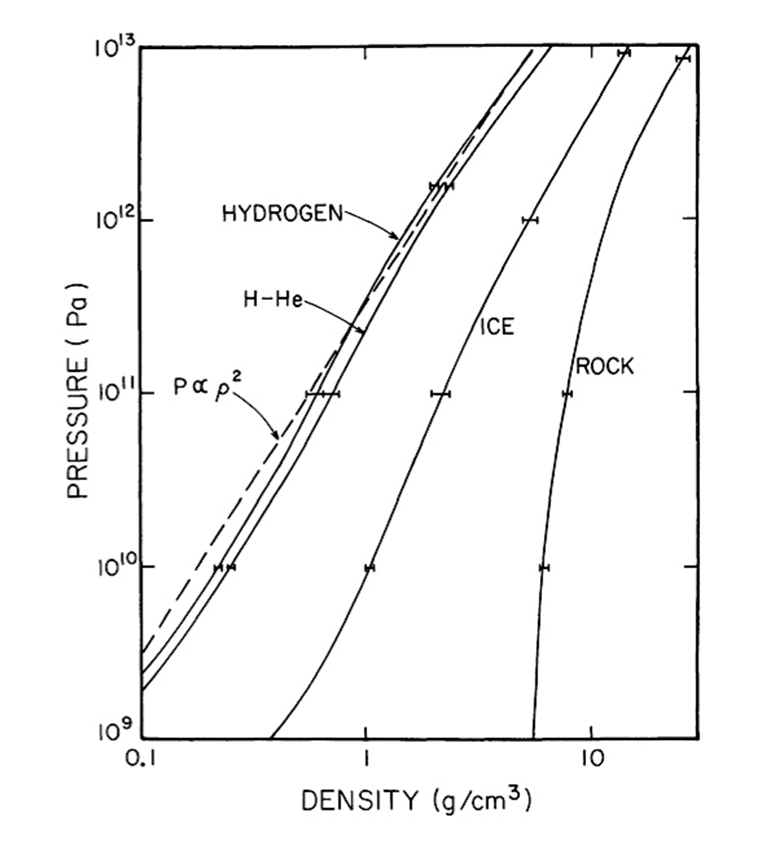
image: Stevenson 1982, AREPS 10, 257

\begin{matrix} \frac{d P}{d r} = 2 K ρ \frac{d ρ}{d r} = - \frac{G M_{r} ρ}{r^{2}} \\ ⟹ r^{2} \frac{d ρ}{d r} = - \frac{G M_{r}}{2 K} \end{matrix}

d M_{r} = 4 π r^{2} ρ (r) d r

\begin{matrix} \frac{d^{2} ρ}{d r^{2}} + \frac{2}{r} \frac{d ρ}{d r} + \frac{2 π G}{K} ρ = 0 \\ ⟹ ρ (r) = ρ_{C} \frac{\sin k r}{k r} \end{matrix}

where, $ρ_{C} =$ central density of the planet, $k = \sqrt{2 π G / K}$

\sin (\sqrt{\frac{2 π G}{K}} r) = 0 ⟹ R = \sqrt{\frac{π K}{2 G}}

for jupiter, it is found that $R = 7.97 \times 10^{7}$ m, which is $= 1.12 R_{J}$ (a really good simple approximation)

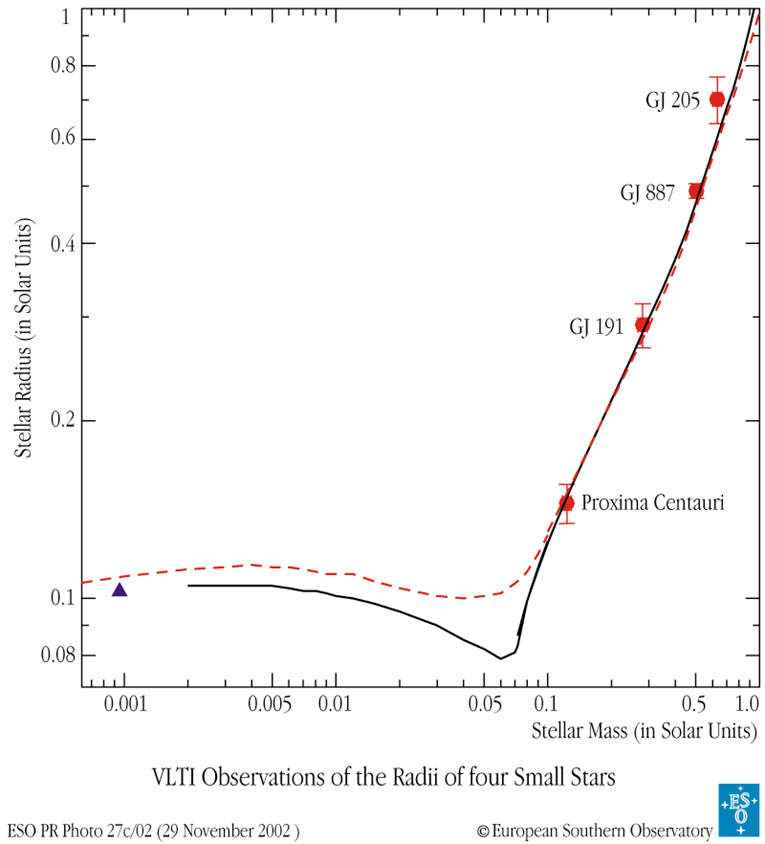
image: ESO 2002

M = \int_{0}^{R} 4 π r^{2} ρ (r) d r = \frac{4 π ρ_{c}}{k} \int_{0}^{R} r \sin k r d r

ρ_{C} = \frac{π M}{4 R^{3}}

for jupiter, $ρ_{C} ≃ 4400$ kg m $^{- 3}$
H/He gas with density similar to rock
from the equation of state, the central pressure: $P_{C} = K ρ_{C}^{2} = 5 \times 10^{12} Pa = 5 \times 10^{7} bar$
the real phase diagram of H implies a metallic liquid at this pressure
the electrons are no longer localised to individual atoms, and it conducts electricity - metallic hydrogen
expect a rocky icy core, then a layer of metallic hydrogen
higher up in the envelope, H transitions to molecular fluid
saturn should have the same layers
but due to lower pressure, the metallic layer is smaller
possible 'rain out' of He, as it forms droplets due to no longer being soluble in H, which drives ongoing differentiation and heating

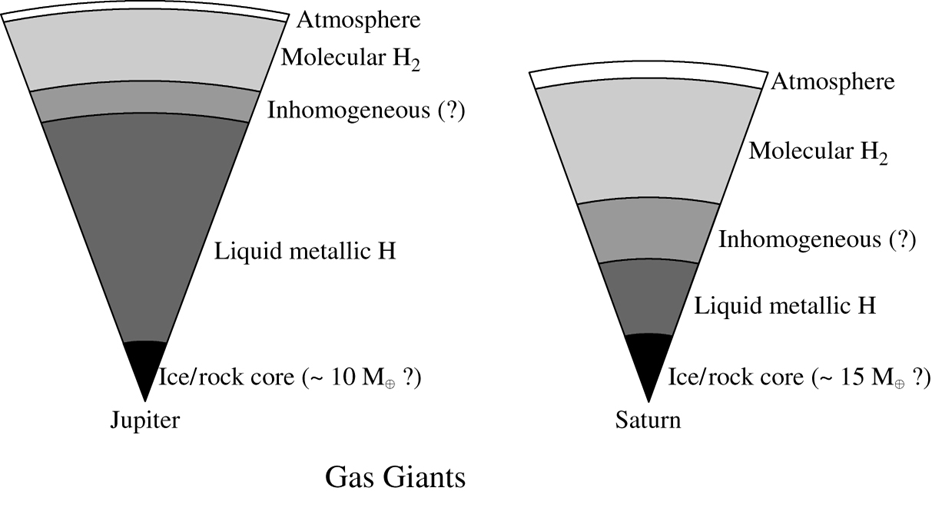
image: Carroll & Ostile, An Introduction to Modern Astrophysics (2007)

both of them rotate rapidly ( $< 0.5$ day, which makes them oblate
this breaks their spherical symmetries
so, the gravitational potential probes the interior structure
eg: samples with juno mission are used for the measurement of $ρ (r)$ , and also north-south asymmetries
the banding pattern extends into deep interior, which implies a global convection

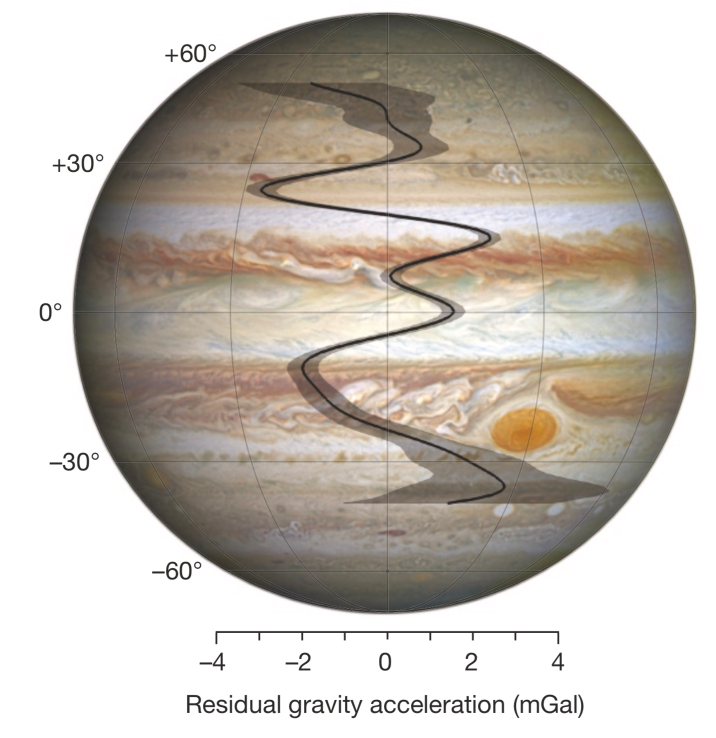
image: IESS, et al 2018

convection, rotation and conducting (metallic) interior forms a magnetic dynamo
therefore, jupiter has a strong magnetic field
the magnetic moment of jupiter $\sim 20000 \times$ that of earth
the magnetic moment of saturn $\sim 600 \times$ that of earth, due to less metallic H
the strong magnetic fields lead to aurorae in poles, as well as radio emissions via both cyclotron and synchrotron emissions by low and high energy electrons orbiting the magnetic field lines

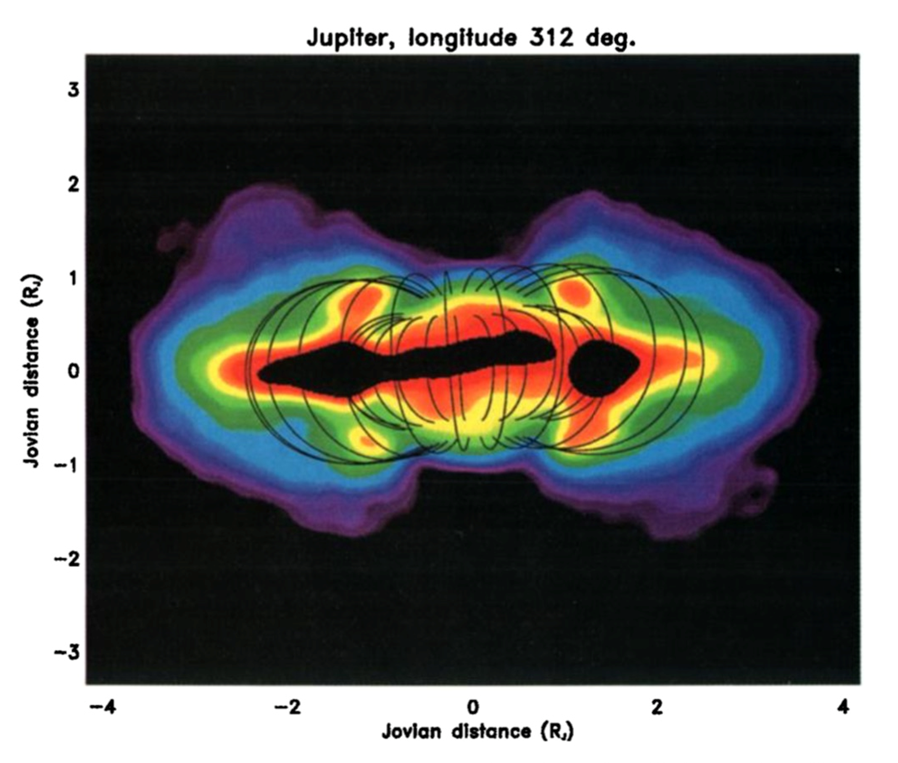
image: de Pater, et al 1997

the combination of strong magnetic moment and lower solar wind flux at $5$ au leads to a very large magnetosphere
the extent can be estimated by equating magnetic energy density $(u_{B})$ with the kinetic energy density of solar winds $(u_{w}) :$

\begin{matrix} u_{B} = \frac{B^{2}}{2 μ_{0}} \\ u_{w} = \frac{1}{2} ρ_{w} v_{w}^{2} \end{matrix}

B (r) = \frac{μ_{0}}{2 π} \frac{μ}{r^{3}}

where, $μ$ is the magnetic dipole moment

\begin{matrix} \frac{μ_{0} μ^{2}}{8 π^{2} r^{6}} = \frac{1}{2} ρ_{w} v_{w}^{2} \\ R_{m} = {(\frac{μ_{0}}{ρ_{w}})}^{1 / 6} {(\frac{μ}{2 π v_{w}})}^{1 / 3} \end{matrix}

where, $R_{m}$ is the radius of the magnetosphere

\begin{matrix} u_{B} \propto {(\frac{μ}{r^{3}})}^{2} \\ u_{w} \propto \frac{1}{a^{2}} \\ \frac{μ}{R_{m}^{3}} \propto \frac{1}{a} ⟹ R_{m} \propto (μ a)^{1 / 3} \end{matrix}

where, $a$ is the orbital separation of the planet

the magnetic dipole moments: $μ_{J} / μ_{E} ≃ 20000$ , and the orbital separations: $a_{J} / a_{E} = 5.2 ⟹ R_{m, J} ≃ 50 R_{m, E}$
$R_{m, E} ≃ 10 R_{E} ⟹ R_{m, J} ≃ 500 R_{E} ≃ 50 R_{J} ≃ 5 R_{⊙}$
so, jupiter's magnetosphere is the largest object in the solar system