PX282 - I6a - three body problem I

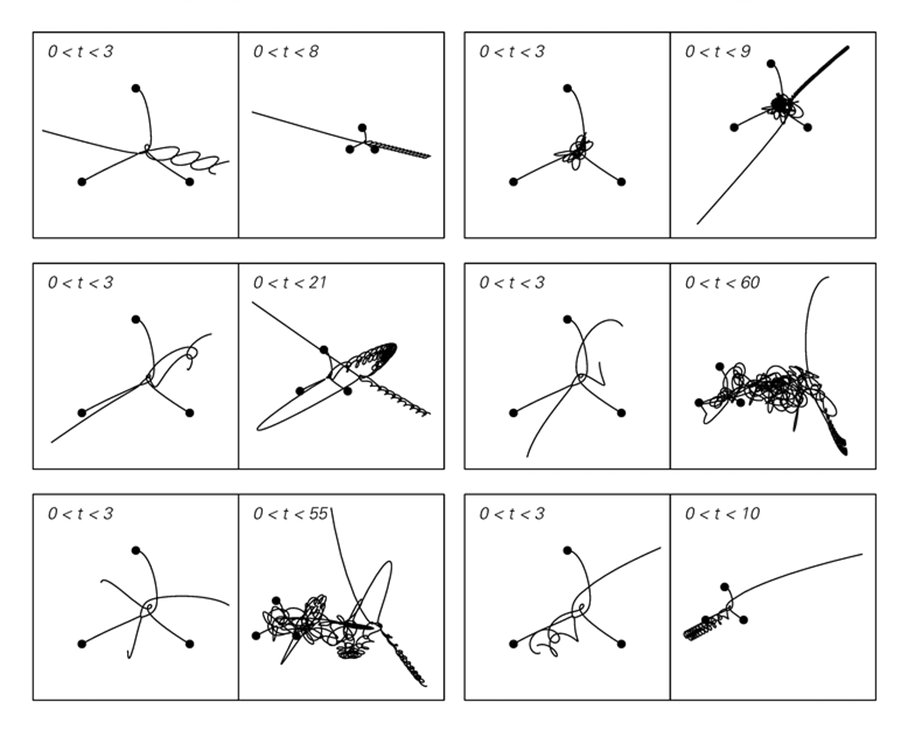
image: Wolfram Alpha

there are exceptions, such as the restricted three body problem, where the mass of third object is negligible

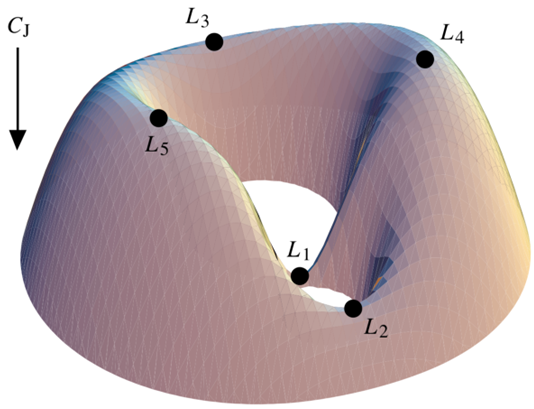
image: Murray & McDermott, Solar System Dynamics (1999)

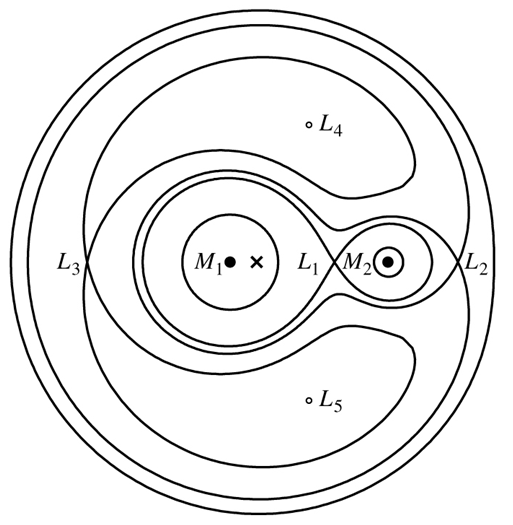
image: Carroll & Ostile, An Introduction to Modern Astrophysics (2007)

stable orbits in roche potential at lagrangian points where the gravitational potential is locally flat (in rotating frame)
eg: $L_{1}$ and $L_{2}$ in earth-sun system is often used for space telescopes

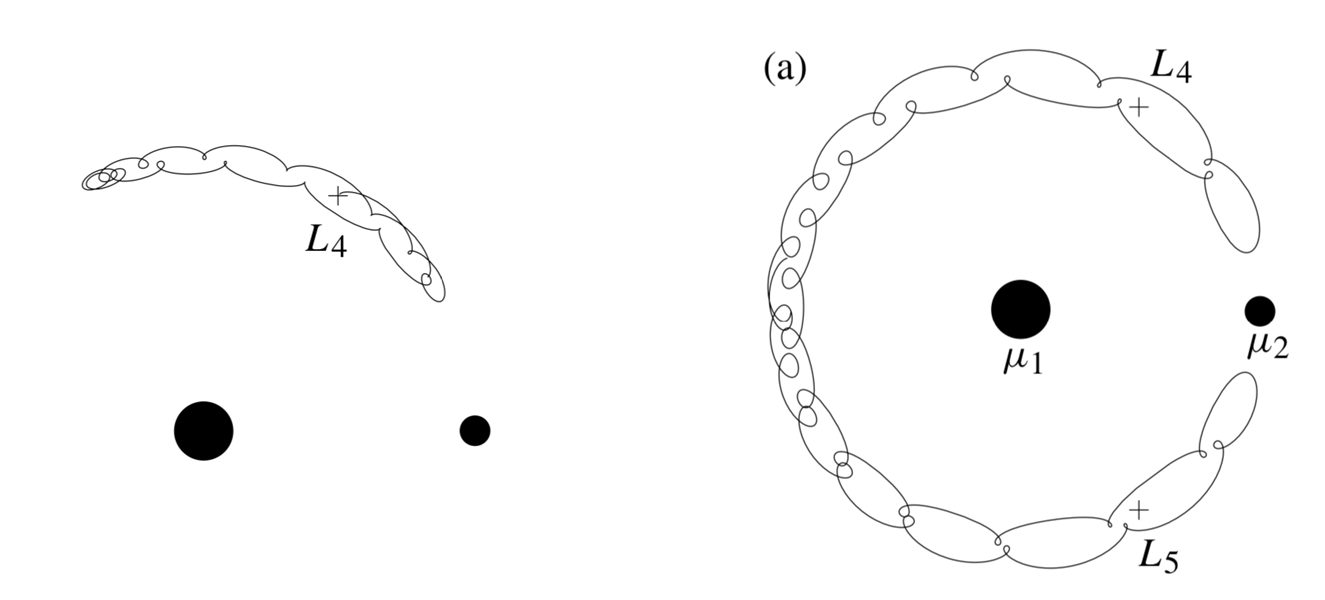
image: Murray & McDermott, Solar System Dynamics (1999)

tadpole and horseshoe orbits vibrate around the $L_{4}$ and $L_{5}$ points
eg: trojan asteroids in jupiter-sun system
approximate sphere of influence around the second body where orbits can be stable, called the hill sphere*
moons must be well within the hill sphere
considering a test particle at $L 1$ point, so the distance between $M_{2}$ and the particle is the radius of the hill sphere, $R_{H}$ , and the distance between $M_{1}$ and $M_{2}$ is $a$

\begin{matrix} \underset{gravitational acceleration}{\underset{⏟}{\frac{G M_{2}}{R_{H}^{2}} - \frac{G M_{1}}{(a - R_{H})^{2}}}} + \underset{centrifugal acceleration}{\underset{⏟}{Ω^{2} (a - R_{H})}} = 0 \end{matrix}

Ω^{2} = {(\frac{2 π}{P})}^{2} = \frac{G m_{1}}{a^{3}}

(a - R_{H})^{- 2} = a^{- 2} {(1 - \frac{R_{H}}{a})}^{- 2} \approx a^{- 2} (1 + 2 \frac{R_{H}}{a})

\begin{matrix} \frac{G M_{2}}{R_{H}^{2}} - \frac{G M_{1}}{a^{2}} (1 + 2 \frac{R_{H}}{a}) + \frac{G M_{1}}{a^{2}} (1 - \frac{R_{H}}{a}) \approx 0 \\ \frac{M_{2}}{R_{H}^{2}} - \frac{M_{1}}{a^{2}} (3 \frac{R_{H}}{a}) \approx 0 \\ ∴ R_{H} \approx {(\frac{M_{2}}{3 M_{1}})}^{1 / 3} a \end{matrix}