PX275 - H7a - convolutions

the convolution of two functions, $f$ and $g$ , is defined as:

f * g (x) = \int_{- \infty}^{\infty} f (y) g (x - y) d y

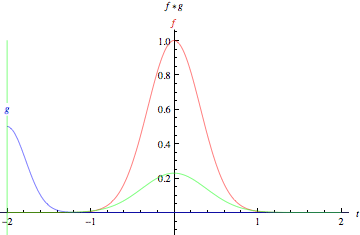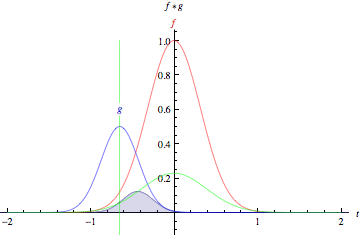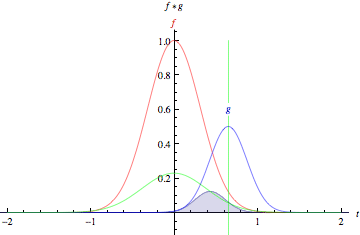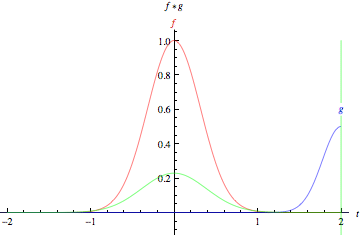
image: Wolfram

fourier transform of a convolution

F (f * g (x)) = \int_{- \infty}^{\infty} f g (x) e^{- i k x} d x = \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} f (y) * g (x - y) e^{- i k x} d x d y

$g (x - y)$ can be rewritten as an inverse fourier transform:

g (x - y) = \frac{1}{2 π} \int_{- \infty}^{\infty} \tilde{g} (k^{'}) e^{i k^{'} (x - y)} d k^{'}

substituting it into the transform:

\begin{aligned} F (f * g (x)) & = \int_{- \infty}^{\infty} e^{- i k x} \int_{- \infty}^{\infty} f (y) \frac{1}{2 π} \int_{- \infty}^{\infty} \tilde{g} (k^{'}) e^{i k^{'} (x - y)} d k^{'} d x d y \\ = ∭_{- \infty}^{\infty} \frac{1}{2 π} e^{i x (k - k^{'})} d x f (y) \tilde{g} (k^{'}) e^{- i k^{'} y} d k^{'} d y \\ = \iint_{- \infty}^{\infty} δ (k - k^{'}) f (y) \tilde{g} (k^{'}) e^{- i k^{'} y} d k^{'} d y \\ = \int_{- \infty}^{\infty} f (y) \tilde{g} (k) e^{- i k y} d y \\ = \tilde{g} (k) \int_{- \infty}^{\infty} f (y) e^{- i k y} d y \\ ∴ F (f * g (x)) & = \tilde{g} (k) \tilde{f} (k) \end{aligned}

therefore, the inverse FT of the product $\tilde{f} (k) \tilde{g} (k)$ must be equal to the convolution:

F (F (f * g)) = f * g

\begin{aligned} f * g (x) & = F^{- 1} (\tilde{f} (k) \tilde{g} (k)) \\ = F^{- 1} (\tilde{g} (k) \tilde{f} (k)) \\ = g * f (x) \end{aligned}

ie. convolutions are symmetric
an alternative definition of a convolution is the inverse fourier transform of a product

\begin{aligned} F^{- 1} (F (f * g (x))) & = F^{- 1} (\tilde{f} (k) \tilde{g} (k)) \\ = \frac{1}{2 π} \int_{- \infty}^{\infty} e^{i k x} \tilde{f} (k) \tilde{g} (k) d k \\ = \frac{1}{2 π} \int_{- \infty}^{\infty} e^{i k x} \int_{- \infty}^{\infty} e^{- i k y} f (y) d y \tilde{g} (k) d k \\ = \int_{- \infty}^{\infty} f (y) \frac{1}{2 π} \int_{- \infty}^{\infty} e^{i k (x - y)} \tilde{g} (k) d k d y \\ = \int_{- \infty}^{\infty} f (y) g (x - y) d y \\ = f * g (x) \end{aligned}