PX275 - H4 - example of fourier transform

eg: $f (x) = δ (x - y)$

\tilde{f} (k) = \int_{- \infty}^{\infty} δ (x - y) e^{- i k x} d x = e^{- i k y}

note: for $y = 0$ , $\tilde{f} (x) = 1$

f (x) = \frac{1}{2 π} \int_{- \infty}^{\infty} e^{i k (x - y)} d k = δ (x - y)

this gives another way to define the dirac delta function as a fourier transform of a complex exponential

δ (x - y) = \frac{1}{2 π} \int_{- \infty}^{\infty} e^{i k (x - y)} d k

\begin{aligned} \tilde{f} (x) & = F (f (x)) \\ f (x) & = F^{- 1} (\tilde{f} (x)) \\ ∴ f (x) & = F^{- 1} (F (f (x))) \end{aligned}

checking:

\begin{aligned} f (x) & = \frac{1}{2 π} \int_{- \infty}^{\infty} \tilde{f} (k) e^{i k x} d k \\ = \underset{F^{- 1} (\tilde{f} (k))}{\underset{⏟}{\frac{1}{2 π} \int_{- \infty}^{\infty} e^{i k x} d k}} \underset{F (f (x^{'}))}{\underset{⏟}{\int_{- \infty}^{\infty} f (x^{'}) e^{- i k x^{'}} d x^{'}}} \\ = \frac{1}{2 π} \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} e^{i k (x - x^{'})} f (x^{'}) d x^{'} d k \\ = \int_{- \infty}^{\infty} f (x^{'}) δ (x - x^{'}) d x^{'} \\ = f (x) \end{aligned}

using a different normalization:

\begin{matrix} \tilde{f} (k) = \frac{1}{a} \int_{- \infty}^{\infty} f (x) e^{- i k x} d x \\ f (x) = \frac{a}{2 π} \int_{- \infty}^{\infty} \tilde{f} (x) e^{i k x} d k \end{matrix}

$a = 1$ was chosen, but a popular choice is $a = \sqrt{2 π}$
$\frac{1}{a} = \frac{1}{\sqrt{2 π}}$
$\frac{a}{2 π} = \frac{1}{\sqrt{2 π}}$
so, both the transforms have the same prefactor

\begin{aligned} F (δ (x - y)) & = e^{i k y} \\ F (δ (x)) & = 1 \end{aligned}

eg: $f (x) = 1 \forall x$

\tilde{f} (k) = \int_{- \infty}^{\infty} e^{- i k x} d x

from the definition of $δ (x - y)$ , and setting $x - y \to - q$ , a dummy variable

δ (- q) = \frac{1}{2 π} \int_{- \infty}^{\infty} e^{- i k q} d k = δ (q)

now, $k \to x^{'} :$

\begin{matrix} δ (q) = \frac{1}{2 π} \int_{- \infty}^{\infty} e^{- i q x^{'}} d x^{'} \\ 2 π δ (q) = \int_{- \infty}^{\infty} e^{- i q x^{'}} d x^{'} \end{matrix}

finally, $q \to k :$

\int_{- \infty}^{\infty} e^{- i k x} d x = 2 π δ (k)

eg: the step function:

f (x) = {\begin{cases} 0 & a < x < b, \\ 1 & elsewhere. \end{cases}

\begin{aligned} \tilde{f} (k) & = \int_{a}^{b} e^{- i k x} d x \\ = - \frac{1}{i k} [e^{- i k x}]_{a}^{b} \\ = - \frac{1}{i k} (e^{- i k b} - e^{- i k a}) \end{aligned}

if $a = - b :$

\begin{aligned} \tilde{f} (k) & = \frac{1}{i k} (e^{i k b} - e^{- i k b}) \\ = \frac{2}{k} \sin k b \\ = 2 b \frac{\sin k b}{k b} \\ = 2 b sinc k b \end{aligned}

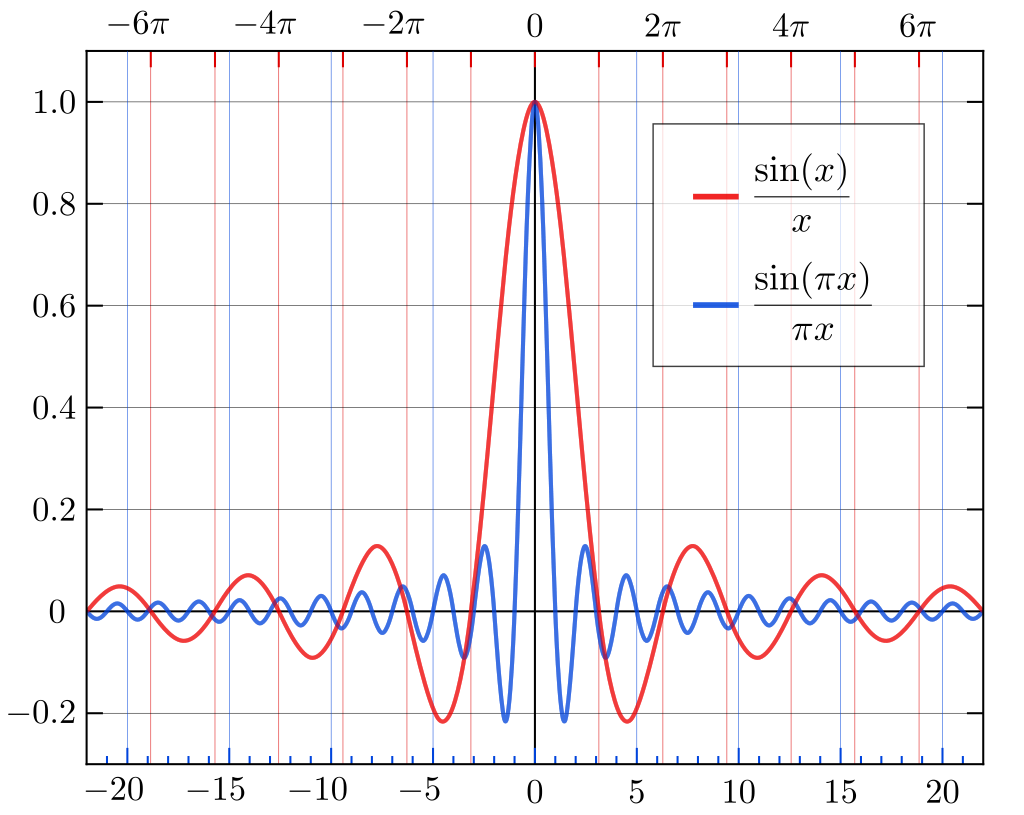
image: Georg-Johann

note to self: see handwritten note for more examples