PX275 - G9 - orthogonality relations

\begin{aligned} \int_{- L}^{L} \cos (\frac{n π x}{L}) \cos (\frac{m π x}{L}) d x & = {\begin{cases} L & if n = m, \\ 0 & if n \neq m \end{cases} \\ \int_{- L}^{L} \sin (\frac{n π x}{L}) \sin (\frac{m π x}{L}) d x & = {\begin{cases} L & if n = m, \\ 0 & if n \neq m \end{cases} \\ \int_{- L}^{L} \sin (\frac{n π x}{L}) \cos (\frac{m π x}{L}) d x & = 0 \end{aligned}

kronecker delta

the kronecker delta is defined as:

δ_{n m} = {\begin{cases} 1 & if n = m, \\ 0 & if n \neq m \end{cases}

application on the string

the PX275 - G6 - boundary and initial conditions:

\begin{matrix} (1) & u (x, 0) = \sum_{n} \sin (\frac{n π x}{L}) C_{n} = f (x) \\ (2) & \frac{\partial u (x, 0)}{\partial t} = \sum_{n} \sin (\frac{n π x}{L}) D_{n} \frac{n π x}{L} = V_{0} δ (x - x_{0}) \end{matrix}

from equation $(1) :$

\begin{aligned} \int_{0}^{L} f (x) \sin (\frac{m π x}{L}) d x & = \sum_{n} C_{n} \int_{0}^{L} \sin (\frac{n π x}{L}) \sin (\frac{m π x}{L}) d x \\ \int_{0}^{L} f (x) \sin (\frac{m π x}{L}) d x & = \sum_{n} C_{n} δ_{n m} \frac{L}{2} \\ \frac{2}{L} \int_{0}^{L} f (x) \sin (\frac{m π x}{L}) d x & = C_{m} \end{aligned}

the initial shape of the string sets $C_{n}$ set of coefficients

initial velocity example 1

consider the function as:

f (x) = {\begin{cases} \frac{2 ϵ}{L} x & for 0 \leq x \leq \frac{L}{2}, \\ \frac{2 ϵ}{L} (L - x) & for \frac{L}{2} \leq x \leq L \end{cases}

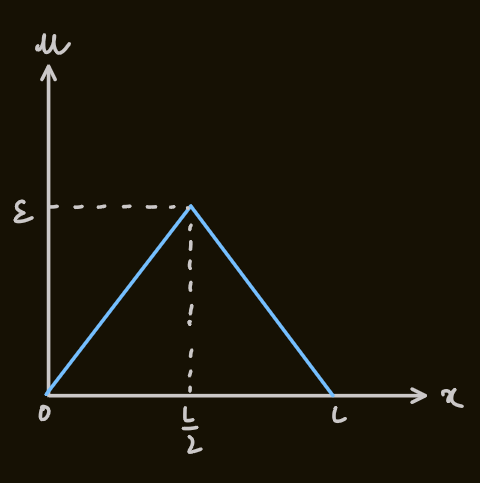
integrating the equation for $C_{n} :$

\begin{aligned} C_{n} & = \frac{4 ϵ}{L^{2}} \int_{0}^{L / 2} x \sin (\frac{n π x}{L}) d x + \frac{4 ϵ}{L^{2}} \int_{L / 2}^{L} (L - x) \sin (\frac{n π x}{L}) d x \\ = \dots \\ = \frac{8 ϵ \sin (n π / 2)}{n^{2} π^{2}} \end{aligned}

∴ u (x, t) = \sum_{n} [\frac{8 ϵ \sin (n π / 2)}{n^{2} π^{2}} \sin (\frac{n π x}{L}) \cos (\frac{n π c t}{L}) + D_{n} \sin (\frac{n π x}{L}) \sin (\frac{n π c t}{L})]

eg: if the string is released from an initial stationary state

\begin{matrix} \frac{\partial u}{\partial t} (x, 0) = 0 \forall x \\ \frac{\partial u}{\partial t} (x, 0) = \sum \sin (\frac{n π x}{L}) D_{n} \frac{n π c}{L} \\ ⟹ D_{n} = 0 \end{matrix}

∴ u (x, t) = \sum_{n} [\frac{8 ϵ \sin (n π / 2)}{n^{2} π^{2}} \sin (\frac{n π x}{L}) \cos (\frac{n π c t}{L})] \propto ϵ / n^{2}

since $\sin \frac{n π}{2} = 0$ for $n \in$ even, only odd harmonics exist

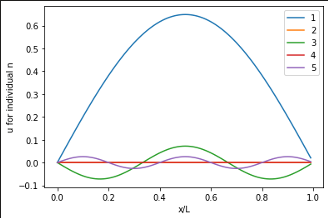
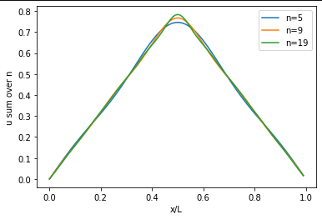
image: A-M Broomhall, lecture notes

initial velocity example 2

\begin{matrix} \frac{\partial u}{\partial t} (x, 0) = \sum_{n} \sin (\frac{n π x}{L}) D_{n} \frac{n π c}{L} = V_{0} δ (x - x_{0}) \\ \int_{0}^{L} \sum_{n} \sin (\frac{n π x}{L}) \sin (\frac{m π x}{L}) D_{n} \frac{n π c}{L} d x = \int_{0}^{L} V_{0} δ (x - x_{0}) \sin (\frac{m π x}{L}) d x \\ \sum_{n} D_{n} \frac{n π c}{L} δ_{n m} \frac{L}{2} = V_{0} \sin (\frac{m π x_{0}}{L}) \\ ∴ D_{m} = \frac{2 V_{0}}{c m π} \sin (\frac{m π x_{0}}{L}) \end{matrix}

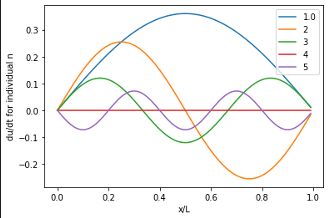
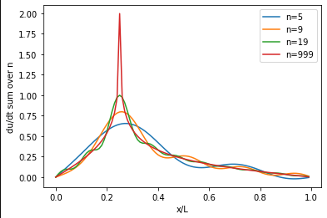
image: A-M Broomhall, lecture notes