PX275 - G6 - boundary and initial conditions

initial conditions

the value of the solution at time, $t = t_{0}$ , or its derivative
eg: initial shape and/or velocity

boundary conditions

physics problems usually directly look at finite domain
dirichlet boundary conditions: values solutions take along boundaries; eg: $u (0, t) = u (L, t)$
neumann boundary conditions: values of derivatives at boundaries; eg: string clamped at both ends
previously:

u (x, t) = (A_{0} x + B_{0}) (C_{0} t + D_{0}) + (A \cos k x + B \sin k x) (C \cos k c x + D \sin k c t)

defining a coordinate frame where the constants of integration vanish
eg: aligning the string with the $x$ -axis, $A_{0} = B_{0} = 0 :$

u (x, t) = (A \cos k x + B \sin k x) (C \cos k c x + D \sin k c t)

taking the boundary condition of string clamped at both ends:

u (0, t) = u (L, t) = 0 \forall t

\begin{matrix} u = A \cos 0 + B \sin 0 = 0 ⟹ A = 0 \\ u = A \cos k L + B \sin k L = 0 ⟹ B \sin k L = 0 \end{matrix}

for this to be true, $k L = n π$ , where $n \in Z$
the solution now reduces to a fourier series:

u (x, t) = \sum_{n} B_{n} \sin k x (C_{n} \cos ω t + D_{n} \sin ω t)

where, $k = n π / L$ and $ω = k c = n π c / L$

recap on fourier series

any function, $f (x)$ , periodic over an interval, $2 L$ , can be described by a fourier series:

f (x) = \frac{a_{0}}{2} + \sum_{n = 1}^{\infty} (a_{n} \cos (\frac{n π x}{L}) + b_{n} \sin (\frac{n π x}{L}))

the average value of the function:

⟨ f (x) ⟩ = \frac{1}{2 L} \int_{- L}^{L} f (x) d x = \frac{a_{0}}{2}

if only interested in the value of the function over a finite domain $(0 \leq x \leq L)$ , it can be periodically extended
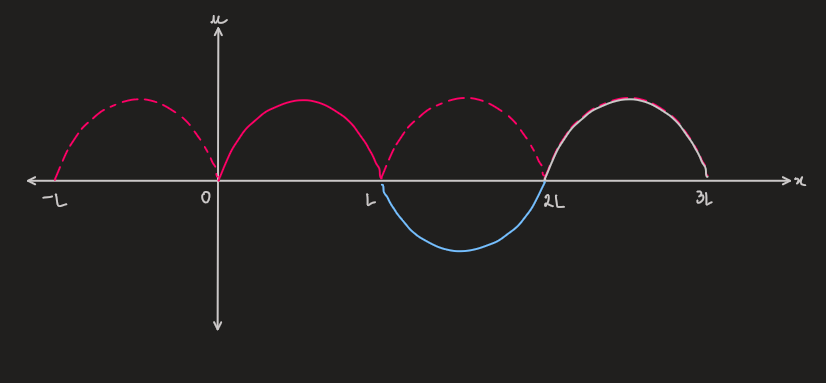
fourier series can thus be used to described non-periodic functions

any solution over a finite domain, eg: $x \in [0, L]$ , can be periodically extended outside of this domain, and thus, a fourier series a a full description of this solution
here, the boundary conditions directly demanded $k = n π / L$ , but the solution can always be written as a fourier series
defining two independent constants:

\begin{matrix} C_{n}^{'} = B_{n} C_{n} \\ D_{n}^{'} = B_{n} D_{n} \end{matrix}

u (x, t) = \sum_{n} \sin (\frac{n π x}{L}) (C_{n}^{'} \cos (\frac{n π c t}{L}) + D_{n}^{'} \sin (\frac{n π c t}{L}))

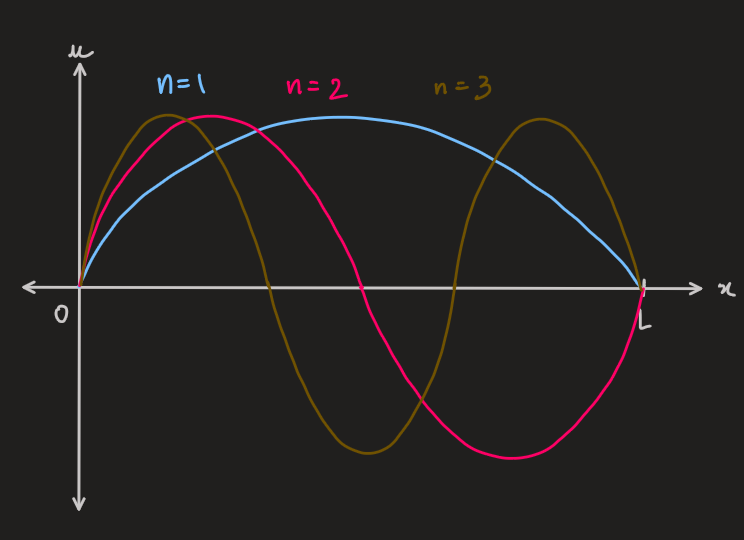
the lowest $n$ corresponds to the longest wavelength and the smallest wavenumber, $k$
initial conditions can describe:
- the shape of the string at $t = 0 :$ $u (x, 0) = f (x)$
- the string is released at $t = 0$ , ie. fully at rest at $t = 0 :$ $\frac{\partial u (x, t)}{\partial t} |_{t = 0} = 0$