PX275 - G3a - diffusion equation

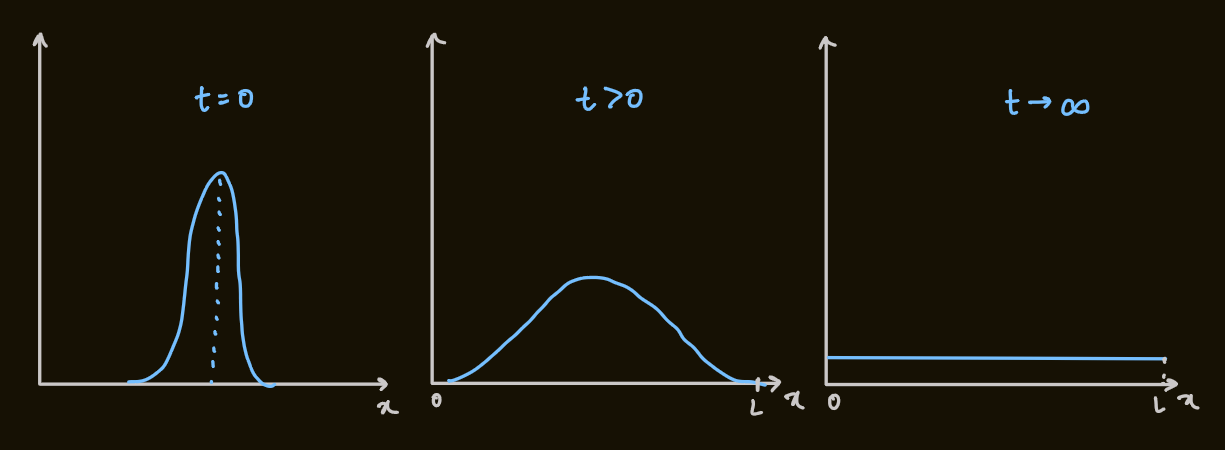
considering the diffusion problem: spatial and temporal variation of a density function, $ρ (x, t)$
with $N$ particles in a volume, $V$ , the volume density, $n = \frac{N}{V}$ , is the number of particles per unit volume (3D)
many cases can be considered in 1D

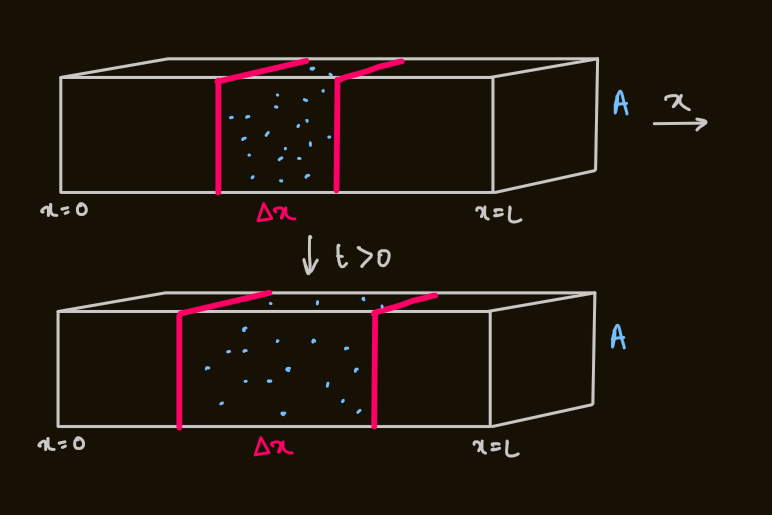
considering a bar of length, $L$ , and cross-section, $A$ , with only one variation in the spatial dimension, say $x$
the concentration of particle: $c = n \times A$
$c (x, t)$ describes the physical (1D) concentration of particles in this medium at $x$ and $t$
the number of particles in the red box: $N = c Δ x$
in general:

N = \int_{0}^{L} c (x, t) d x

if there is no source or sink, $N$ is constant

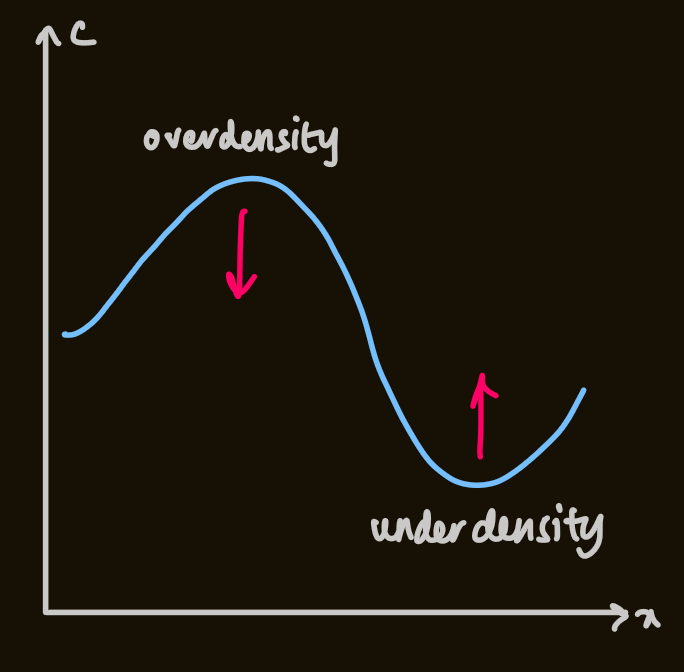
diffusion acts to reduce gradients in concentration
gradients will lead to a flux of particles

considering the particle flux, $j (x)$ , then the net flux $=$ number of particles moving right - number of particles moving left
fick's law:

j (x) \propto - \frac{\partial c}{\partial x}

where, $j (x)$ is the local flux at $x$ , and the negative sign works to reduce the gradient, $\frac{\partial c}{\partial x}$

the proportionality constant is defined to be $D$ , the diffusivity of the medium:

j (x) = - D \frac{\partial c}{\partial x}

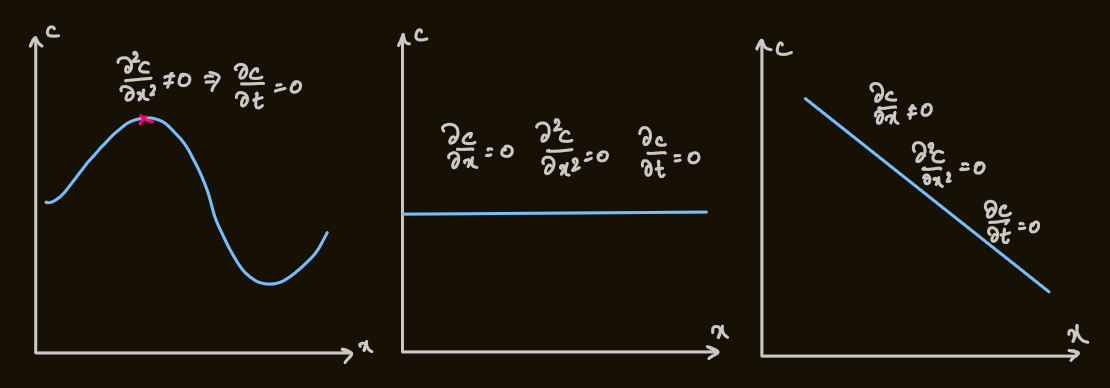
the continuity must be satisfied
considering a small part, $Δ x$
the change in the number of particles over $Δ x$ at a fixed time:

Δ j = j (x, t) - j (x + Δ x, t)

over time, $Δ t :$

\begin{matrix} (1) & Δ j Δ t = [j (x, t) - j (x + Δ x, t)] Δ t \end{matrix}

recalling that $N = c Δ x$ , so the change in the number within $Δ x$ across time, $Δ t$ , is:

\begin{matrix} (2) & - [c (x, t) - c (x, t + Δ t)] Δ x \end{matrix}

combining equation $(1)$ and $(2) :$

\begin{matrix} [j (x, t) - j (x + Δ x, t)] Δ t = - [c (x, t) - c (x, t + Δ t)] Δ x \\ Δ j Δ t = - Δ x Δ c \end{matrix}

lim_{Δ x, Δ t \to 0} \frac{\partial j}{\partial x} = - \frac{\partial c}{\partial t}

from fick's law:

\frac{\partial c}{\partial t} = D \frac{\partial^{2} c}{\partial x^{2}}

this is the diffusion equation for a 1D concentration field, $c (x, t)$ , in a medium with a constant diffusivity, $D$

dimensions of the diffusion constant

[\frac{\partial c}{\partial t}] = [T]^{- 1} a n d [\frac{\partial^{2} c}{\partial x^{2}}] = [L]^{- 2}

∴ [D] = [L]^{2} [T]^{- 1}

it has been assumed that $D$ is constant
if $D$ is not constant:

\frac{\partial c}{\partial t} = \frac{\partial}{\partial x} (D (x) \frac{\partial c}{\partial x})

if there is a source or sink of particles:

\frac{\partial c}{\partial t} = \frac{\partial}{\partial x} (D \frac{\partial c}{\partial x}) + S (x, t)