PX275 - F1 - tensors

considering the angular momentum of a simple system:

\vec{L} = I \vec{ω}

where, $I$ is the moment of inertia, and $\vec{ω}$ is the angular velocity

considering two masses, $m_{1}$ and $m_{2}$ , on the end of a stiff rod with negligible mass, attached to a string, and making an angle, $θ$ , to the horizontal
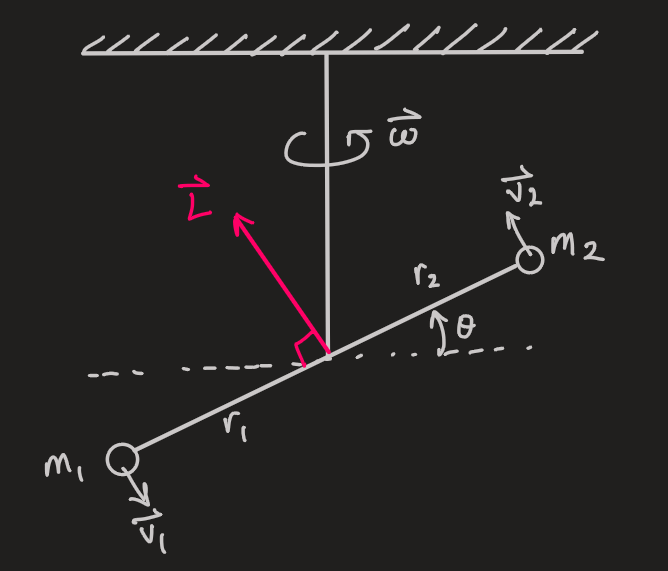
the angular momentum of masses in general:

\vec{L} = \vec{r} \times \vec{p} = m (\vec{r} \times \vec{v})

the total angular momentum:

\vec{L} = {\vec{L}}_{1} + {\vec{L}}_{2}

for the system of two masses:

\vec{L} = \sum_{i = 1}^{2} {\vec{r}}_{i} \times {\vec{p}}_{i} = \sum_{i = 1}^{2} m_{i} ({\vec{r}}_{i} \times {\vec{v}}_{i}) $ $ $ $ \vec{L} = \sum_{i = 1}^{2} m_{i} ({\vec{r}}_{i} \times ({\vec{ω}}_{i} \times {\vec{r}}_{i}))

for one mass:
$\vec{r} = x \hat{i} + y \hat{j} + z \hat{k}$
$\vec{ω} = ω_{x} \hat{i} + ω_{y} \hat{j} + ω_{z} \hat{k}$

\begin{aligned} \vec{ω} \times \vec{r} & = | \begin{array}{c} \hat{i} & \hat{j} & \hat{k} \\ ω_{x} & ω_{y} & ω_{z} \\ x & y & z \end{array} | \\ = (ω_{y} z - ω_{z} y) \hat{i} + (ω_{z} x - ω_{x} z) \hat{j} + (ω_{x} y - ω_{y} x) \hat{k} \end{aligned}

hence, the angular momentum:

\begin{matrix} \vec{r} \times (\vec{ω} \times \vec{r}) = \\ ((y^{2} + z^{2}) ω_{x} - (x y) ω_{y} - (x z) ω_{z}) \hat{i} \\ + ((- x y) ω_{x} + (x^{2} + z^{2}) ω_{y} - (y z) ω_{z}) \hat{j} \\ + ((- x z) ω_{x} - (y z) ω_{y} + (x^{2} + y^{2}) ω_{z}) \hat{k} \end{matrix}

the boxed terms represent the principal moments of inertia
the components of the angular momentum vector can be written as:

\begin{array}{r} L_{x} = ω_{x} I_{x x} + ω_{y} I_{x y} + ω_{z} I_{x z} \\ L_{y} = ω_{x} I_{y x} + ω_{y} I_{y y} + ω_{z} I_{y z} \\ L_{z} = ω_{x} I_{z x} + ω_{y} I_{z y} + ω_{z} I_{z z} \end{array}

in matrix notation:

[\begin{matrix} L_{x} \\ L_{y} \\ L_{z} \end{matrix}] = [\begin{matrix} I_{x x} & I_{x y} & I_{x z} \\ I_{y x} & I_{y y} & I_{y z} \\ I_{z x} & I_{z y} & I_{z z} \end{matrix}] [\begin{matrix} ω_{x} \\ ω_{y} \\ ω_{z} \end{matrix}]

this can be written more concisely as:

L_{j} = \sum_{i = 1, 2, 3} I_{i j} {\vec{ω}}_{j}

where, $L_{1} = L_{x}$ , and so on

L_{1} = (I_{11} + I_{21} + I_{31}) ω_{x} = I_{i j} ω_{x}

$I$ is the moment of inertia tensor, a $2^{n d}$ rank/order tensor with $9$ components