PX275 - D3a - green's theorem in the plane

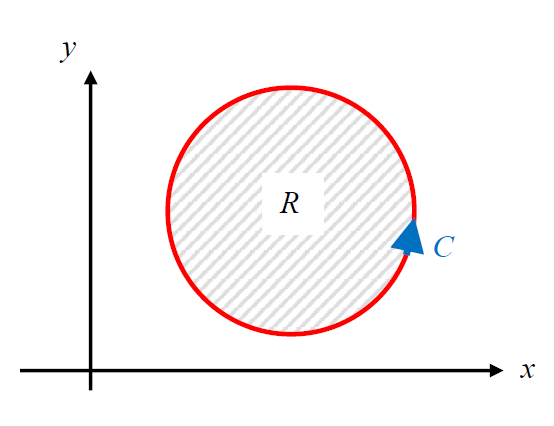
green's theorem relates an integral around a closed loop to an integral over the area of the region enclosed by the loop
this is a two dimensional theorem, but it underpins the divergence and stokes' theorems
considering a vector field in 2D:

\vec{F} = P (x, y) \hat{i} + Q (x, y) \hat{j}

where, $P$ and $Q$ are scalar functions of $(x, y)$

taking a path from $A$ to $B$ in the $x - y$ plane:

\int_{A}^{B} \vec{F} \cdot d \vec{r} = \int_{A}^{B} (P \hat{i} + Q \hat{j}) \cdot (d x \hat{i} + d y \hat{j}) = \int_{A}^{B} P d x + Q d y

considering a closed loop:

\oint_{C} \vec{F} \cdot d \vec{r} = \oint_{C} P d x + Q d y

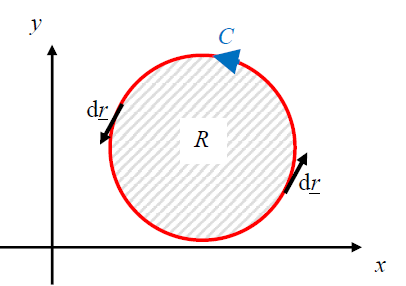
green's theorem relates the integral of a vector field around a loop to the integral of the differentiated components of that field over the area enclosed by the loop:

\oint_{C} \vec{F} \cdot d \vec{r} = \oint_{C} P d x + Q d y = \iint_{R} (\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}) d A

for a conservative field, the loop integral will be zero, and hence, so is the $R H S$ of green's theorem:

\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} = 0

\iint_{R} (\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}) = \iint_{R} (\vec{\nabla} \times \vec{F})_{z} d A

extending it to three dimensions gives stokes' theorem:

\oint_{C} \vec{F} \cdot d \vec{r} = \iint_{R} (\vec{\nabla} \times \vec{F}) \cdot d \vec{A}

where, $d A$ is a vector element, normal to the plane where $(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y})$ is being calculated