PX275 - D2b - conservative vector fields

conditions

I = \int \vec{a} \cdot d \vec{r}

the path dependence of the integral depends on the definition of $\vec{a}$
for a conservative vector field, the integral is path independent
a vector field must be continuous (partial derivatives) and simply connected (no holes)
a vector field is said to be conservative if:
- the path integral, $\int \vec{a} \cdot d \vec{r}$ , is independent of the path taken $^{†}$
- there exists a scalar function, $ϕ$ , such that the vector field can be expressed as the gradient of the scalar function, ie: $\vec{a} = \vec{\nabla} ϕ$
- it has no curl, ie: $\vec{\nabla} \times \vec{a} = 0$
- $\vec{a} \cdot d \vec{r}$ is an exact differential, ie: $\oint \vec{a} \cdot d \vec{r} = 0$
note: validity of any one of the above four conditions means that the others are also valid
consider a vector field, $\vec{a} = \vec{\nabla} ϕ$ , if $\vec{a}$ is conservative:

\int_{A}^{B} \vec{a} \cdot d \vec{r} = ϕ (B) - ϕ (A)

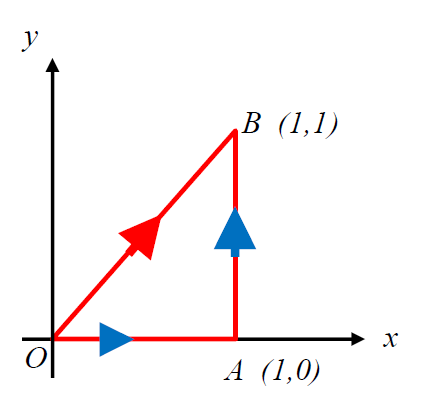
previously considered:
taking 2 paths in each case:
- $O A B$
- $O B$
considering $\vec{G} :$
- for path $O A B :$
$\int_{O A B} \vec{G} \cdot d \vec{r} = \int_{x = 0}^{x = 1} x \hat{i} \cdot d x \hat{i} + \int_{y = 0}^{y = 1} x \hat{i} \cdot d y \hat{j} = \frac{1}{2}$
- for path $O B :$
$\int_{O B} \vec{G} \cdot d \vec{r} = \int_{O B} x \hat{i} \cdot (d x \hat{i} + d y \hat{j}) = \int_{x = 0}^{x = 1} x d x = \frac{1}{2}$
considering $\vec{H} :$
- for path $O A B :$
$\int_{O A B} \vec{H} \cdot d \vec{r} = \int_{x = 0}^{x = 1} x \hat{j} \cdot d x \hat{i} + \int_{y = 0, x = 1}^{y = 1} x \hat{j} \cdot d y \hat{j} = 1$
- for path $O B :$
$\int_{O B} \vec{H} \cdot d \vec{r} = \int_{O B} x \hat{j} \cdot (d x \hat{i} + d y \hat{j}) = \int_{y = 0, x = y}^{y = 1} x d y = \frac{1}{2}$
this is sufficient proof to show that $\vec{H}$ is non-conservative, but not to show that $\vec{G}$ is conservative as all paths need to be considered
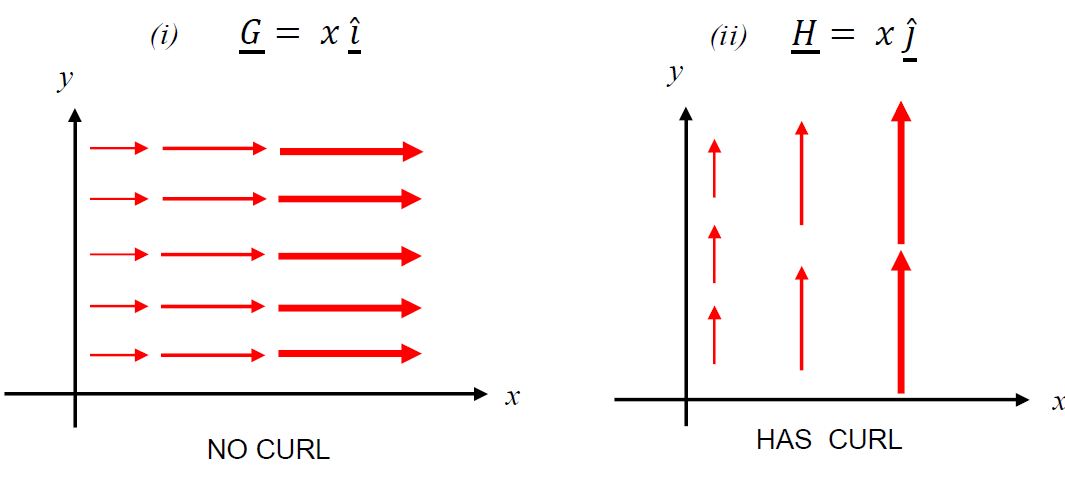
$\vec{G}$ does not have curl, therefore it is conservative, and has no path-dependence
$\vec{H}$ has curl, therefore the integral has path-dependence

past paper [2021 Q1]

\vec{F} = \frac{- y}{x^{2} + y^{2}} \hat{i} + \frac{x}{x^{2} + y^{2}} \hat{j}

\begin{aligned} \vec{\nabla} \times \vec{F} & = | \begin{array}{c} \hat{i} & \hat{j} & \hat{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ \frac{- y}{x^{2} + y^{2}} & \frac{x}{x^{2} + y^{2}} & 0 \end{array} | \\ = [\frac{\partial}{\partial x} (\frac{x}{x^{2} + y^{2}}) - \frac{\partial}{\partial y} (\frac{- y}{x^{2} + y^{2}})] \hat{k} \\ = [\frac{1}{x^{2} + y^{2}} \frac{- 2 x^{2}}{(x^{2} + y^{2})^{2}} - (\frac{1}{x^{2} + y^{2}} \frac{- 2 y^{2}}{(x^{2} + y^{2})^{2}})] \hat{k} \\ \vec{\nabla} \times \vec{F} & = 0 \end{aligned}

\begin{aligned} \oint_{C} \vec{F} \cdot d \vec{r} & = \oint (\frac{- y}{x^{2} + y^{2}} \hat{i} + \frac{x}{x^{2} + y^{2}} \hat{j}) \cdot (- r \sin ϕ d p h i \hat{i} + r \cos ϕ d ϕ \hat{j}) \\ = \oint (\frac{y \sin ϕ}{x^{2} + y^{2}} + \frac{x \cos ϕ}{x^{2} + y^{2}}) r d ϕ \\ = \oint d ϕ \\ = 2 π \end{aligned}