PX262 - H4 - free electron model (3D)
- now, considering a box of dimensions:
- applying periodic boundary conditions:
- from the first condition:
- similarly:
- therefore, the wavevector:
where,
- the allowed states sit on a grid in wavevector-space
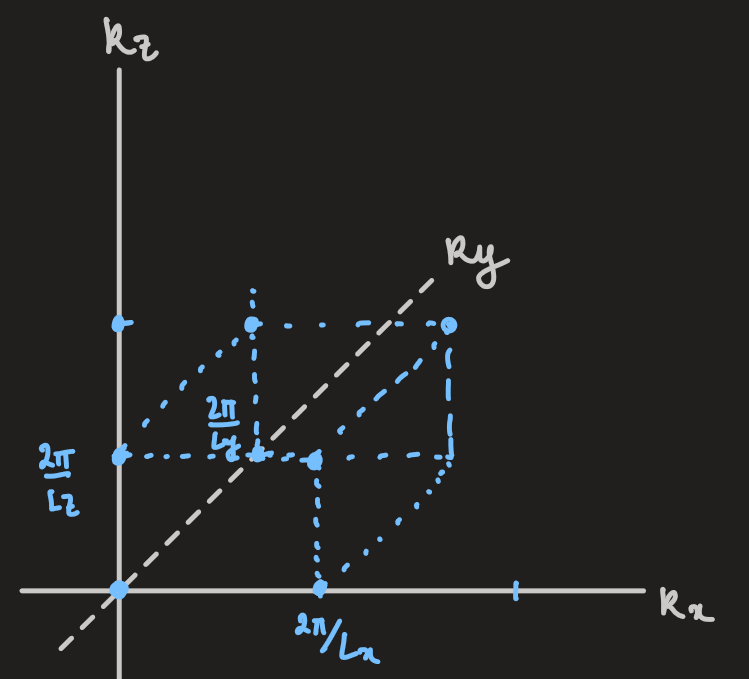
- each block, contains one allowed
vector (each corner shared between eight blocks)
- these single electron states can be occupied by two electrons: spins
and - ground state: fill all states (
and ) up to or
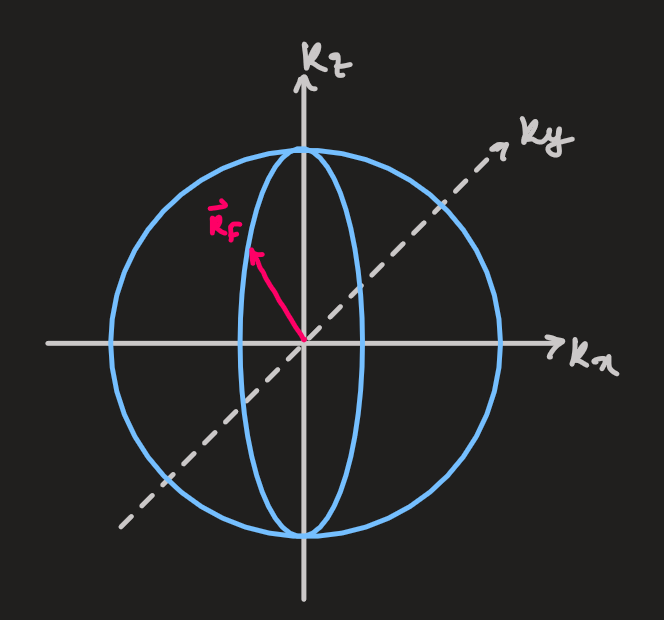
- occupied states lie in a sphere in the k-space
- total number of electrons:
where, 2 is for each spin
where,
is the radius of the fermi sphere, and also the magnitude of the fermi wavevector, - fermi wavevector and fermi energy are set by the density,
- also, the fermi velocity:
- and the fermi speed:
- this is the group velocity of the wave packet with
grouped around
density of states
- for a large
, it is expected that: , forming a continuum of states in the space of (k-space) - the number of states with an energy below
- the number of states between
and
ie. the density of states:
- let
can be used to compute some properties - the simplest is the total energy:
- the average energy per particle:
(m |
(eV) |
(Å |
(ms |
|
|---|---|---|---|---|
| Li | ||||
| Al |
- the free fermion model is relevant in other areas:
- white dwarfs:
eV - neutron stars:
eV
- white dwarfs:
temperatue
note:
- introducing
, probability of states with energy, , are occupied
.png)
- for a non-zero
, is given by the fermi-dirac distribution (FD):
where,
- in metals,
- strictly:
heat capacity
- can argue that some electrons in states below
thermally excited to states above number of excitations , where - assuming the variation of
within of negligible
- assuming the variation of
- the heat capacity:
- linear dependence of
on is characteristic of metals