PX262 - H3 - free electron model (1D)

loosely bound valence electrons $(\sim 10^{24})$ in a metal are modelled as non-interacting fermions in a potential form a uniform, positively charged background, so the system charge is neutral
putting a large number of electrons, $N$ , in a large box

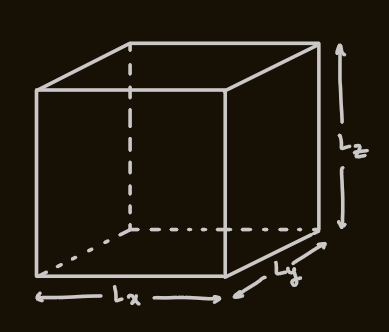
considering a 1D case
feeding in $N$ electrons with two per state (spin $↑, ↓$ ) to find the ground state energy:

N = 2 n_{F}

where, $F$ stands for fermi

and the wavenumber of the highest occupied state, the fermi wavenumber is:

k_{F} = \frac{n_{F} π}{L} = \frac{N π}{2 L} = \frac{π}{2} ρ_{e}

where, $ρ_{e}$ is the density, $N / L$

the energy of the highest occupied state, the fermi energy is:

E_{F} = \frac{ℏ^{2} k_{F}^{2}}{2 m} = \frac{ℏ^{2}}{2 m} {(\frac{N π}{2 L})}^{2} = \frac{ℏ^{2} π^{2}}{8 m_{e}} ρ_{e}^{2}

for a large $N$ , large $L$ , it is useful to impose periodic boundary conditions instead and consider running wave solutions: $ϕ (x) = A e^{i k x}$

ϕ (x) = ϕ (x + L) = ϕ (x + 2 L) = \dots

this means that $e^{i k L} = 1$ and $k L = 2 π n$ with $n = \pm 1, \pm 2, \dots$

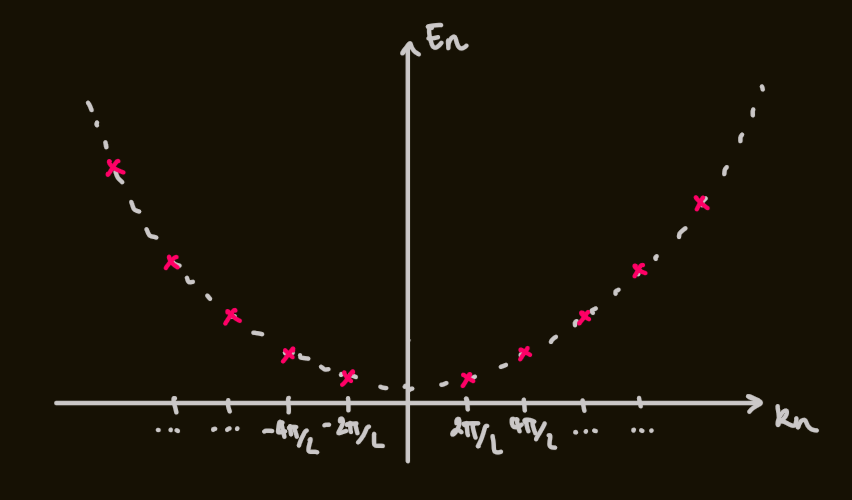
the energy levels are given as:

E_{n} = \frac{ℏ^{2}}{2 m_{e}} k_{n}^{2}

and the states are:

ϕ_{n} (x) = A e^{i k_{n} x}

the wavenumbers are separated by $\frac{2 π}{L}$
to account for both positive and negative:

N = 2 \times 2 n_{F} = 4 n_{F}

\begin{matrix} k_{F} = \frac{N}{4} \frac{2 π}{L} = \frac{π}{2} ρ_{e} \\ N = \frac{2 L}{π} k_{F} \end{matrix}

the fermi energy:

E_{F} = \frac{ℏ^{2}}{2 m_{e}} {(\frac{N π}{2 L})}^{2} = \frac{ℏ^{2} π^{2}}{8 m_{e}} ρ_{e}^{2}

the number of states with energies less than a given value, $E_{n} \leq E_{F} :$

N (E_{n}) = \frac{2 L}{π} k_{n} = \frac{2 L}{π} {(\frac{2 m_{e}}{ℏ^{2}})}^{1 / 2} E_{n}^{1 / 2}

in a large, effectively infinite system, $L \to \infty$ , there is a continuum of states

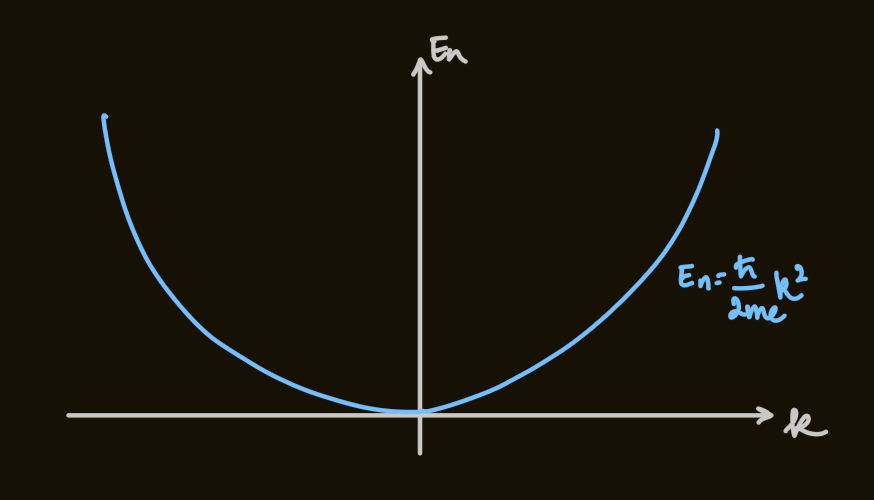
note: the states are distributed with respect to energy:

N (E + Δ E) ≃ N (E) + \frac{d N}{d E} Δ E = N (E) + n (E) Δ E

where, $n (E)$ is the density of states (DOS)

PX284 - H1 - density of states (DOS)

sometimes, $g (E)$ is used to denote the DOS

n (E) = \frac{L}{π} {(\frac{2 m_{e}}{ℏ^{2}})}^{1 / 2} \frac{1}{\sqrt{E_{F}}}

this can be used to calculate properties:
the total energy:

\begin{aligned} E_{T O T} & = \int_{0}^{E_{F}} E n (E) d E (= \sum_{n + 1}^{N / 2} E_{n = 2}) \\ = \frac{L}{π} {(\frac{2 m_{e}}{ℏ^{2}})}^{1 / 2} \int_{0}^{E_{F}} \frac{E}{\sqrt{E}} d E \\ = \frac{L}{π} {(\frac{2 m_{e}}{ℏ})}^{1 / 2} \frac{2}{3} E_{F}^{3 / 2} \end{aligned}

the average energy per electron:

E_{e v} = \frac{E_{T O T}}{N} = \frac{E_{F}}{3}