PX262 - H2 - quantum mechanics and many particles

in classical mechanics, for several particles $(N)$ , the kinetic and the potential energies are given by:

\begin{matrix} T = \sum_{i = 1}^{N} \frac{p_{i}^{2}}{2 m_{i}} \\ V = V ({\vec{r}}_{1}, {\vec{r}}_{2}, \dots) \end{matrix}

in quantum mechanics, the system is defined by a wavefunction, which is a function of the positions and spins of the particles:

ψ ({\vec{r}}_{1}, σ_{1}; {\vec{r}}_{2}, σ_{2}; \dots {\vec{r}}_{N,} σ_{N}, t)

it must satisfy the schrödinger equation:

\hat{H} ψ = i ℏ \frac{\partial ψ}{\partial t}

$\hat{H}$ is the hamiltonian operator:

\hat{H} = \sum_{i = 1}^{N} (\frac{{\hat{p}}_{i}^{2}}{2 m} + \hat{V})

where, ${\hat{p}}_{i} = - i ℏ \vec{\nabla}$ is the momentum operator

for identical particles, $ψ$ is either symmetric or antisymmetric
it is symmetric when the coordinates of any two particles are swapped if they are bosons (eg: $π$ -mesons, phonons, photons, etc)

\begin{matrix} ψ ({\vec{r}}_{1}, σ_{1}; \dots {\vec{r}}_{a}, σ_{a}; \dots \dots {\vec{r}}_{b}, σ_{b}; \dots {\vec{r}}_{N,} σ_{N}, t) \\ = ψ ({\vec{r}}_{1}, σ_{1}; \dots {\vec{r}}_{b}, σ_{b}; \dots \dots {\vec{r}}_{a}, σ_{a}; \dots {\vec{r}}_{N,} σ_{N}, t) \end{matrix}

and it is antisymmetric when the particles are fermions (eg: electrons, protons, etc)

\begin{matrix} ψ ({\vec{r}}_{1}, σ_{1}; \dots {\vec{r}}_{a}, σ_{a}; \dots \dots {\vec{r}}_{b}, σ_{b}; \dots {\vec{r}}_{N,} σ_{N}, t) \\ = - ψ ({\vec{r}}_{1}, σ_{1}; \dots {\vec{r}}_{b}, σ_{b}; \dots \dots {\vec{r}}_{a}, σ_{a}; \dots {\vec{r}}_{N,} σ_{N}, t) \end{matrix}

this captures the pauli exclusion principle: no two electrons can occupy the same state
eg: putting several non-interacting electrons in a box (1D)
the single electron is bound by: $0 < x < L$
the energy is given by:

- \frac{ℏ}{2 m} \frac{d^{2}}{d x^{2}} ϕ (x) = E ϕ (x)

the solutions are in the form:

ϕ (x) = A e^{i k x} + B e^{- i k x} = C \cos (k x) + D \sin (k x)

trapping the electron in the box:
$ϕ (0) = 0 ⟹ C = 0$
$ϕ (L) = 0 ⟹ k L = n ϕ$ , $n \in Z$
therefore, the wavenumbers:

k_{n} = \frac{n π}{L}

and the energies:

E_{n} = \frac{ℏ}{2 m_{e}} {(\frac{n π}{L})}^{2}

the states:

ϕ_{n} = D \sin (\frac{n π x}{L})

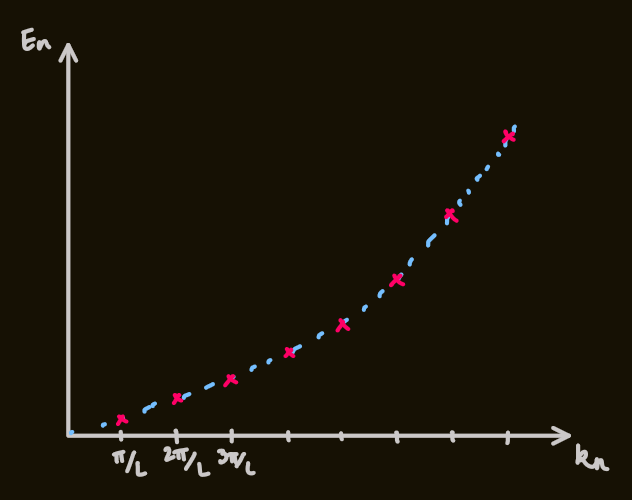
the ground state energy, $E_{g}$ , for a system of several electrons, using the pauli exclusion principle:

E_{g} = E_{1} + E_{1} + E_{2} + E_{2} + \dots

where, the two $E_{1}$ terms are for spin $↑$ and spin $↓$