PX262 - F5 - particle in a spherical potential well

considering that the particle is bound to be within a sphere, the potential energy would be:

V (r) = {\begin{cases} 0 & r \leq a \\ \infty & r > a \end{cases}

the radial schrödinger equation: $- \frac{ℏ^{2}}{2 m} \frac{d^{2} χ}{d r^{2}} + [V (r) + \frac{ℏ^{2}}{2 m r^{2}} l (l + 1)] χ = E χ$
solving it for this potential: $- \frac{ℏ^{2}}{2 m} \frac{d^{2} χ}{d r^{2}} + \frac{ℏ^{2}}{2 m r^{2}} l (l + 1) χ = E χ$
setting a constant: $k^{2} = \frac{2 m E}{ℏ^{2}}$ , and transforming: $x = k r :$ $\frac{d^{2} R (x)}{d x^{2}} + \frac{2}{x} \frac{d R (x)}{d x} + [1 - \frac{l (l + 1)}{x^{2}}] R (x) = 0$
this is well known in mathematics as the spherical bessel equation and has solutions in the form of spherical bessel functions, $j_{l} (x)$ , and spherical neumann functions, $n_{l} (x) :$

\begin{aligned} j_{0} (x) & = \frac{\sin x}{x} \\ j_{1} (x) & = \frac{\sin x}{x} - \frac{\cos x}{x} \\ j_{2} (x) & = (\frac{3}{x^{2}} - \frac{1}{x}) \sin x - \frac{3}{x^{2}} \cos x \\ n_{0} & = - \frac{\cos x}{x} \end{aligned}

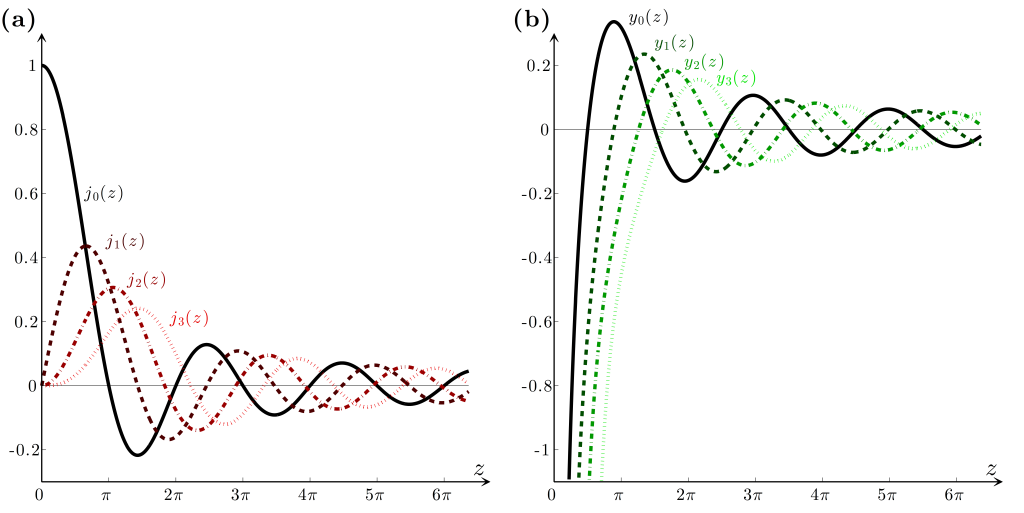
imgae: P. H. Jones, O. M. Maragò & G. Volpe
spherical bessel functions (left), and spherical neumann functions (right)

spherical neumann functions diverge at $x = 0$ , and thus, they cannot describe a wavefunction as it cannot be normalized
therefore, spherical bessel functions are the only valid solutions
imposing the boundary condition, $R (a) = 0$ , ie: $j_{l} (k a) = 0$
the spherical bessel functions are zero at many points
denoting the position of the $n^{t h}$ crossing of zero by $x_{n l}$ , the energy levels are:
$E_{n, l} = \frac{ℏ^{2} x_{n l}^{2}}{2 π a^{2}}$
the wavefunction:
$ϕ_{n l m} = j_{n l} (\frac{x_{n l} r}{a}) Y_{l, m} (θ, ϕ)$
there are three quantum numbers, $n, l, m$
states with different $n$ and/or $l$ will have different energies