PX262 - E2 - eigenvalues and eigenfunctions

\begin{matrix} x = r \sin θ \cos ϕ \\ y = r \sin θ \sin ϕ \\ z = r \cos θ \\ \vec{\nabla} = \hat{r} \frac{\partial}{\partial r} + \frac{1}{r} \hat{θ} \frac{\partial}{\partial θ} + \frac{1}{r \sin θ} \hat{ϕ} \frac{\partial}{\partial ϕ} \end{matrix}

\begin{matrix} \hat{r} \times \hat{r} = 0 \\ \hat{θ} \times \hat{r} = - \hat{ϕ} \\ \hat{ϕ} \times \hat{r} = \hat{θ} \end{matrix}

\begin{aligned} \hat{\vec{L}} = - i ℏ \hat{\vec{r}} \times \vec{\nabla} & = - ℏ (\hat{ϕ} \frac{\partial}{\partial θ} - \frac{1}{\sin θ} \hat{θ} \frac{\partial}{\partial ϕ}) \\ ⟹ {\hat{L}}_{z} & = \hat{z} \cdot \hat{\vec{L}} = - i ℏ \frac{\partial}{\partial ϕ} \end{aligned}

the angular momentum squared operator can be expressed using the vector identity:

\begin{aligned} {\hat{L}}^{2} & = - ℏ^{2} (\hat{r} \times \vec{\nabla}) \cdot (\hat{r} \times \vec{\nabla}) \\ = - ℏ^{2} \hat{r} \cdot [\vec{\nabla} \times (\hat{r} \times \vec{\nabla})] \\ = - ℏ^{2} [\frac{1}{\sin θ} \frac{\partial}{\partial θ} (\sin θ \frac{\partial}{\partial θ}) + \frac{1}{\sin^{2} θ} \frac{\partial^{2}}{\partial ϕ^{2}}] \end{aligned}

\begin{aligned} {\hat{L}}^{2} Y & = λ Y \\ {\hat{L}}_{z} Y & = ν Y \end{aligned}

\begin{aligned} - i ℏ \frac{\partial}{\partial ϕ} Θ (θ) Φ (ϕ) & = ν Θ (θ) Φ (ϕ) \\ - i ℏ \frac{\partial Φ (ϕ)}{\partial ϕ} & = ν Φ (ϕ) \end{aligned}

the general solution for this equation is: $Φ = C \exp (\frac{i ν ϕ}{ℏ})$ where $C$ is the normalization constant
with $ϕ$ being the angle, the answer should stay the same after a rotation by $2 π$ , ie: $Φ (ϕ + 2 π) = Φ (ϕ)$
therefore, it is required that $\frac{ν}{ℏ} = m$ , where $m$ is an integer
normalizing the function:

\begin{aligned} 1 & = \int_{0}^{2 π} Φ^{*} Φ d ϕ \\ = C^{2} \int_{0}^{2 π} e^{i m ϕ} e^{- i m ϕ} d ϕ \\ = C^{2} 2 π \\ ∴ C & = \frac{1}{\sqrt{2 π}} \end{aligned}

therefore, the eigenfunctions have the form:
$Φ = \frac{1}{\sqrt{2 π}} e^{i m ϕ}$
where the eigenvalues would be: $ν = ℏ m$
with $ϕ$ -dependence fixed, looking at ${\hat{\vec{L}}}^{2} :$

\begin{aligned} - ℏ^{2} [\frac{1}{\sin θ} \frac{\partial}{\partial θ} (\sin θ \frac{\partial}{\partial θ}) + \frac{1}{\sin^{2} θ} \frac{\partial^{2}}{\partial ϕ^{2}}] Θ (θ) Φ (ϕ) & = λ Θ (θ) Φ (ϕ) \\ - ℏ^{2} [\frac{1}{\sin θ} Φ (ϕ) \frac{\partial}{\partial θ} (\sin θ \frac{\partial Θ (θ)}{\partial θ}) + \frac{Θ (θ)}{\sin^{2} θ} \frac{\partial^{2} Φ (ϕ)}{\partial ϕ^{2}}] & = λ Θ (θ) Φ (ϕ) \\ - ℏ^{2} [\frac{1}{\sin θ} Φ (ϕ) \frac{\partial}{\partial θ} (\sin θ \frac{\partial Θ (θ)}{\partial θ}) + \frac{Θ (θ)}{\sin^{2} θ} (- m^{2} Φ (ϕ))] & = λ Θ (θ) Φ (ϕ) \\ - ℏ^{2} \sin θ \frac{d}{d θ} (\sin θ \frac{d Θ (θ)}{d θ}) + ℏ^{2} Θ (θ) m^{2} - λ \sin^{2} θ Θ (θ) & = 0 \end{aligned}

substituting $v = \cos θ :$ $\frac{d}{d θ} = - \sin θ \frac{d}{d v} = - (1 - v^{2})^{\frac{1}{2}} \frac{d}{d v}$
$Θ (θ)$ can be rewritten as $P (v) :$ $ℏ^{2} \frac{d}{d v} [(1 - v^{2})^{\frac{1}{2}} \frac{d P (v)}{d v}] + [λ - \frac{ℏ^{2} m^{2}}{1 - v^{2}}] = 0$
solving explicitly for $m = 0$ , looking at the solution in the form:

P (v) = \sum_{p = 0}^{\infty} a_{p} v^{p}

following the same logic as for the harmonic oscillator, substituting $P$ into the differential equation will lead to a recursive relation between coefficients
it will be found that the expansion diverges at $v = 1$ , so, the coefficients after some value of $p$ must be cut off
this can be done by setting: $λ = ℏ^{2} l (l + 1)$ where, $l$ is a positive integer
the functions, $P (v)$ , are well known polynomials, legendre polynomials
the first few legendre polynomials are:

\begin{aligned} P_{0} (v) & = 1 \\ P_{1} (v) & = v \\ P_{2} (v) & = \frac{1}{2} (3 v^{2} - 1) \\ P_{3} (v) & = \frac{1}{2} (5 v^{3} - 3 v) \end{aligned}

functions for $m \neq 0$ follow the same steps, but the maths is quite complicated, hence the details are skipped
the solutions in terms of $P (v)$ are given by functions:

P_{l}^{| m |} (v) = (1 - v^{2})^{| m | / 2} \frac{d^{| m |} P_{l}}{d v^{| m |}}

if $| m | > l$ , the derivative will be zero, and the whole wavefunction will be zero over all space, which is physically unrealistic
therefore the values of $m$ are restricted by the condition:

| m | \leq l

the eigenfunctions of ${\hat{L}}^{2}$ and ${\hat{L}}_{z}$ are:
$Y_{l m} (θ, ϕ) = (- 1)^{m} {[\frac{2 l + 1}{4 π} \frac{(l - | m |)!}{(l + | m |)!}]}^{1 / 2} P_{l}^{| m |} (\cos θ) \exp (i m ϕ)$
where, $(- 1)^{m}$ is purely a convention
the functions, $Y_{l m} (θ, ϕ)$ , are called spherical harmonics
the factor in the brackets is the normalization factor such that:
$\int_{0}^{2 π} \int_{0}^{π} | Y_{l m} (θ, ϕ) |^{2} \sin θ d θ d ϕ = 1$
these functions are orthogonal and form a complete set, so any general wavefunction can be written as a linear combination of $Y_{l m} (θ, ϕ)$
the eigenvalue equations are:

\begin{aligned} {\hat{L}}_{z} Y_{l, m} (θ, ϕ) & = ℏ m Y_{l, m} (θ, ϕ) \\ {\hat{L}}^{2} Y_{l m} (θ, ϕ) & = ℏ^{2} l (l + 1) Y_{l m} (θ, ϕ) \end{aligned}

$l$ and $m$ are often used as quantum numbers to label states, referred to as orbital and magnetic quantum numbers respectively
spherical harmonics for $l \leq 2 :$

\begin{aligned} Y_{00} (θ, ϕ) & = \frac{1}{\sqrt{4 π}} \\ Y_{10} (θ, ϕ) & = \mp \sqrt{\frac{3}{4 π}} \cos θ \\ Y_{1 \pm 1} (θ, ϕ) & = \mp \sqrt{\frac{3}{8 π}} \sin θ e^{\pm i ϕ} \\ Y_{20} (θ, ϕ) & = \mp \sqrt{\frac{5}{16 π}} (3 \cos^{2} θ - 1) \\ Y_{2 \pm 1} (θ, ϕ) & = \mp \sqrt{\frac{15}{8 π}} \cos θ \sin θ e^{\pm i ϕ} \\ Y_{2 \pm 2} (θ, ϕ) & = \mp \sqrt{\frac{15}{32 π}} \sin^{2} θ e^{\pm 2 i ϕ} \end{aligned}

for two neighbouring states with the same $l$ , $Δ m = m_{1} - m_{2}$ , is constant
another analogue of ladder operators can be defined for angular momentum operator as:

\begin{aligned} {\hat{L}}_{+} & = {\hat{L}}_{x} + i {\hat{L}}_{y} \\ {\hat{L}}_{-} & = {\hat{L}}_{x} - i {\hat{L}}_{y} \end{aligned}

{\hat{L}}_{\pm} Y_{l, m} (θ, ϕ) = \sqrt{(l \mp m) (l \pm m + 1)} ℏ Y_{l, m + 1} (θ, ϕ)

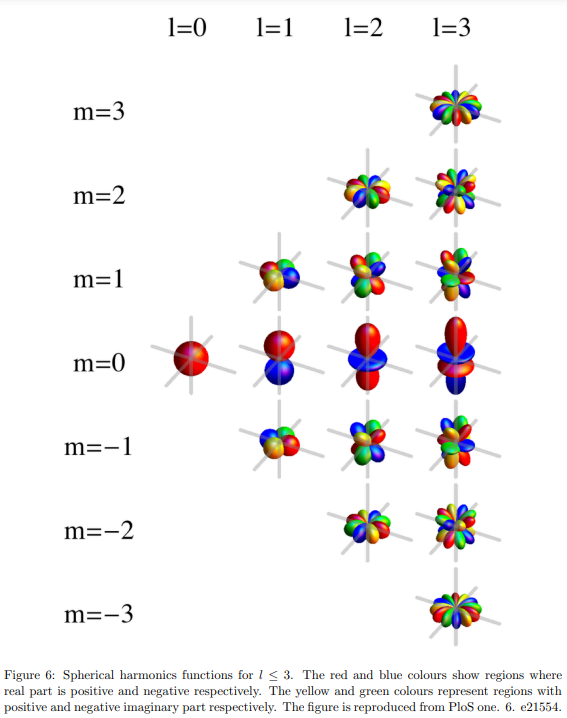
image: Q. Wang, K. Birod, C. Angioni, et al. PLoS ONE 6(7): e21554. https://doi.org/10.1371/journal.pone.0021554