PX262 - C4 - probability distributions

taking the lowest energy state of a particle in an infinite potential well, and its wavefunction
the position eigenfunctions are defined by the dirac delta functions, and the whole wavefunction could be viewed as a sum of an infinite number of these functions
considering a experiment where the particle is found in one of a series of detectors of width, $Δ$
if the particle is measured in a particular detector, the wavefunction will be non-zero everywhere except on that detector, with a peak $h$ and width, $Δ$
the height is given by the fact that the probability of finding the particle in that strip is one:
$h^{2} Δ = 1 ⟹ h = Δ^{- \frac{1}{2}}$
note: $h^{2}$ comes from the fact that probability comes from $| ψ |^{2}$
the $n^{t h}$ wavefunction is denoted by $ϕ_{n}$ , which is properly normalized
the wavefunction before such measurement is $ψ$
if $ψ (x)$ is divided into a strips of width, $Δ$ , which can be approximated by $ψ (x_{n})$ inside the $n^{t h}$ strip

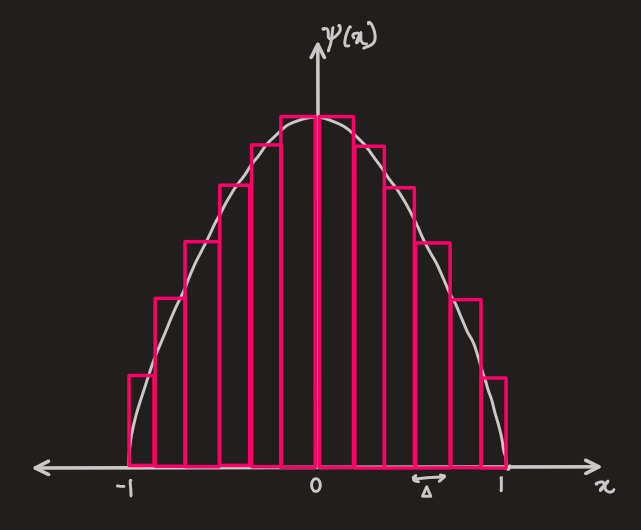
$ϕ_{n}$ would represent a strip of height $h$ covering the strip, and is zero outside it:

ψ (x) = \sum_{n} \frac{ψ (x_{n})}{h} ϕ_{n} = \sum_{n} a_{n} ϕ_{n}

where,

a_{n} = \frac{ψ (x_{n})}{h} = Δ^{1 / 2} ψ (x_{n})

the weights correspond to the probability of finding the particle in each strip
the probability of finding the particle in the $n^{t h}$ strip is: $P (x_{n}) = | ψ (x_{n}) |^{2} Δ = | a_{n} |^{2}$
generalising to any measurement by the operator $\hat{Q} :$ $ψ = \sum_{n} a_{n} ϕ_{n}$
this exploits the property of hermitian operators that their wavefunctions form a complete set, and that any well-behaved function can be expressed as a liner superposition of the eigenfunctions