PX262 - B6 - 1D harmonic oscillator

in classical physics: $V (x) = \frac{1}{2} k x^{2}$ where, $k$ is the spring constant, $x$ is the displacement from the equilibrium position
a particle with a mass, $m$ , will be oscillating with an angular frequency, $ω_{c} = \sqrt{\frac{k}{m}}$
the time independent schrödinger equation:

\begin{aligned} - \frac{ℏ^{2}}{2 m} \frac{d^{2} ϕ (x)}{d x} + \frac{1}{2} m ω_{c}^{2} x^{2} ϕ (x) & = E ϕ (x) \\ \frac{d^{2} ϕ (y)}{d y^{2}} + (α - y^{2}) ϕ (y) = 0 \end{aligned}

where, $y = \sqrt{\frac{M ω_{c}}{ℏ}} x$ , and $α = \frac{2 E}{ℏ ω_{c}}$

\frac{d^{2} ϕ}{d y^{2}} - y^{2} ϕ = 0

\begin{matrix} ϕ = y^{n} e^{- \frac{y^{2}}{2}} \\ ⟹ \frac{d ϕ}{d y} = n y^{n - 1} e^{- \frac{y^{2}}{2}} - y e^{- \frac{y^{2}}{2}} = \frac{n}{y} ϕ (y) - y ϕ (y) \\ ⟹ \frac{d^{2} ϕ}{d y^{2}} = - \frac{n}{y^{2}} ϕ (y) + \frac{n}{y} (\frac{n}{y} ϕ (y) - y ϕ (y)) - ϕ (y) - y (\frac{n}{y} ϕ (y) - y ϕ (y)) \\ = \frac{n (n - 1)}{y^{2}} ϕ (y) - (2 n + 1) ϕ (y) + y^{2} ϕ (y) \end{matrix}

\frac{d^{2} ϕ (y)}{d y^{2}} \approx y^{2} ϕ (y)

- also, $ϕ \approx 0$ due to the $e^{\frac{- y^{2}}{2}}$ term

for all values of $y$ , the general solution can be written as: $ϕ (y) = H (y) e^{- \frac{y^{2}}{2}}$ where, $H (y)$ is a function that needs to be determined
substituting $H$ in the TISE: $H^{″} - 2 y H^{'} + (α - 1) H = 0$
any well behaved wavefunctions in quantum mechanics can be written as a power series: $H (y) = \sum_{p = 0}^{\infty} a_{p} y^{p}$ where, $a_{p}$ is constant to be determined
differentiating $H :$

\begin{aligned} H^{'} & = \sum_{p = 1}^{\infty} a_{p} p y^{p - 1} \\ H^{″} & = \sum_{p = 1}^{\infty} a_{p} p (p - 1) y^{p - 2} \\ = \sum_{p = 2}^{\infty} a_{p} p (p - 1) y^{p - 2} \\ = \sum_{p^{'} = 0}^{\infty} a_{p^{'} + 2} (p^{'} + 2) (p^{'} + 1) y^{p^{'}} \end{aligned}

\begin{matrix} \sum_{p = 0}^{\infty} [(p + 1) (p + 2) a_{p + 2} - (2 p + 1 - α)] y_{p} = 0 \\ (p + 1) (p + 2) a_{p + 2} - (2 p + 1 - α) a_{p} = 0 \\ \frac{a_{p + 2}}{a_{p}} = \frac{2 p + 1 - α}{(p + 1) (p + 2)} \end{matrix}

$H$ will tend to $e^{y^{2}}$ , which diverges as $y \to \infty :$
$⟹ ϕ (y) = e^{\frac{- y^{2}}{2}} e^{y^{2}} = e^{\frac{y^{2}}{2}}$
this cannot describe a valid wavefunction as the integral would be infinite
the number of contributing terms need to be restricted by stopping the sum at some point
this can be done by making all constants, $a_{p} = 0$ for $p > n$
setting the numerator, $2 n + 1 - α = 0 ⟹ α = 2 n + 1$
substituting the value of $α$ gives the allowed energies:
$E_{n} = (n + \frac{1}{2}) ℏ ω_{c}$
the condition $α = 2 n + 1$ removed even/odd terms, but not both
the lowest state has $n = 0$ , and its energy is called the zero-point energy:
$E_{0} = \frac{1}{2} ℏ ω_{c}$
the energy levels are evenly spaced with the difference, $ℏ ω_{c}$
the polynomials $H (y)$ are called hermite polynomials:

\begin{matrix} H_{0} = 1 & H_{1} = 2 y \\ H_{2} = 4 y^{2} - 2 & H_{3} = 8 y^{3} - 12 y \end{matrix}

\begin{aligned} ϕ_{0} & = {(\frac{M ω}{ℏ π})}^{\frac{1}{4}} \exp (\frac{- M ω x^{2}}{2 ℏ}) \\ ϕ_{1} & = {(\frac{4}{π})}^{\frac{1}{4}} {(\frac{M ω}{ℏ π})}^{\frac{1}{4}} \exp (\frac{- M ω x^{2}}{2 ℏ}) \\ ϕ_{2} & = {(\frac{M ω}{4 π ℏ})}^{\frac{1}{4}} [\frac{2 M ω}{ℏ} x^{2} - 1] \exp (\frac{- M ω x^{2}}{2 ℏ}) \end{aligned}

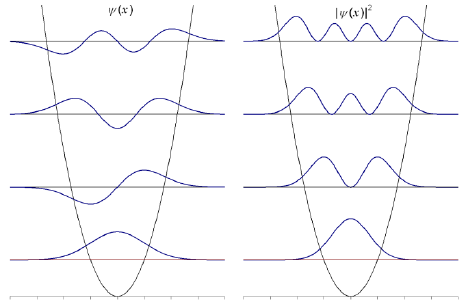
image: avtar sehra