PX262 - B4 - particle in an infinite square well

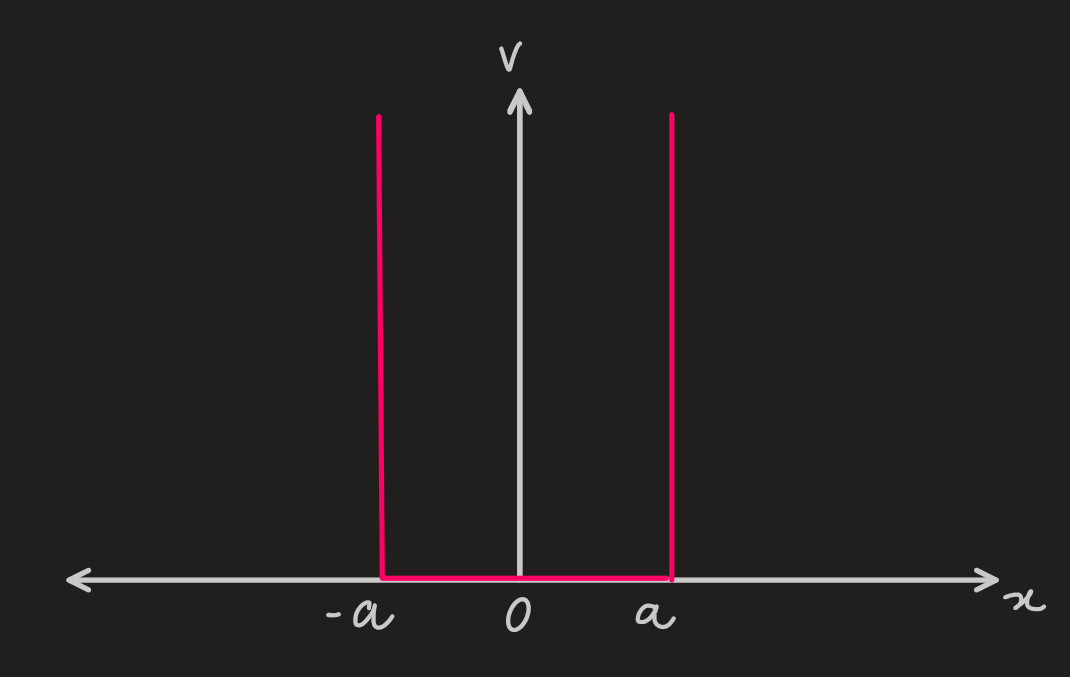
considering an infinite square potential well:
$V (x) = {\begin{cases} 0 & f o r & | x | < a, \\ \infty & f o r & | x | > a . \end{cases}$
infinite potential means that particles cannot be in that region, ie: $ϕ = 0$
inside the well:
$- \frac{ℏ^{2}}{2 m} \frac{d^{2} ϕ (x)}{d x^{2}} = E ϕ (x)$
the solution has the form: $ϕ (x) = A \cos (k x) + B \sin (k x)$
where, $A$ and $B$ are constants, and $k = \sqrt{\frac{2 m E}{ℏ^{2}}}$
the boundary conditions require that the function is continuous at the border of the potential well: $ϕ (- a) = ϕ (a) = 0$

\begin{matrix} A \cos (k a) + B \sin (k x) = 0 \\ A \cos (- k a) + B \sin (- k x) = 0 \\ 2 A \cos (k a) = 0 \\ 2 B \sin (k a) = 0 \end{matrix}

two options to satisfy this:
- $B = 0$ , $\cos (k a) = 0 ⟹ k = \frac{n π}{2 a}, n \in o d d$
- $A = 0$ , $\sin (k a) = 0 ⟹ k = \frac{n π}{2 a}, n \in e v e n$
wave function (after normalization):

ϕ_{n} (x) = {\begin{cases} \frac{1}{\sqrt{a}} \cos (\frac{n π x}{2 a}) & for n \in odd, \\ \frac{1}{\sqrt{a}} \sin (\frac{n π x}{2 a}) & for n \in even, \\ 0 & for | x | > a . \end{cases}

- the index in the labels give the state of the system

\begin{matrix} E_{n} = \frac{ℏ^{2} π^{2}}{8 m a^{2}} n^{2} \end{matrix}

note:
- a particle in the system can only have specific, discrete energies
- the probabilities of finding the particle at different positions will depend on the energies
typical values for electron, $m = 9.1 \times 10^{- 31} k g$ , in an atom of size, $10^{- 10} m :$ $E_{n} = 9.4 e V n^{2}$
more macroscopic: $m = 10^{- 10} k g$ ; $a = 10^{- 6} m ⟹ E_{n} = 1.4 \times 10^{- 46} n^{2} J$
- thermal energy at $1 K \sim 10^{- 23} J$ , $n$ must be $3 \times 10^{11}$
- differences between energies and positions are so small that they cannot be distinguished experimentally
correspondence principle: when going towards macroscopic objects, the quantum mechanical description will result in something resembling classical physics