PX158 - PS4

Q1

The most distant objects discovered in the Solar System are around 90 au from the Sun. Assuming that they behave as blackbodies, estimate their temperatures.

\begin{aligned} π R^{2} \frac{L_{⊙}}{4 π d^{2}} & = 4 π R^{2} σ T^{4} \\ T & = {(\frac{L_{⊙}}{16 π σ d^{2}})}^{\frac{1}{4}} \\ T & \approx 29 K \end{aligned}

Q2

It has been suggested that one could combat global warming by placing mirrors in orbit around Earth to reflect some of the Sun’s radiation away from Earth. Calculate the total mirror area required to lower Earth’s temperature by 1K.

\begin{aligned} (π R^{2} - A) \frac{L_{⊙}}{4 π d^{2}} & = 4 π R^{2} σ T^{4} \\ (1 - \frac{A}{π R^{2}}) π R^{2} \frac{L_{⊙}}{4 π d^{2}} & = 4 π R^{2} σ T^{4} \\ (1 - \frac{A}{π R^{2}}) 4 π R^{2} σ T_{0}^{4} & = 4 π R^{2} σ T^{4} \\ \frac{A}{π R^{2}} & = 1 - {(\frac{T}{T_{0}})}^{4} \\ \approx 0.014 \\ ∴ A & = 1.75 \times 10^{6} k m^{2} \end{aligned}

Q3

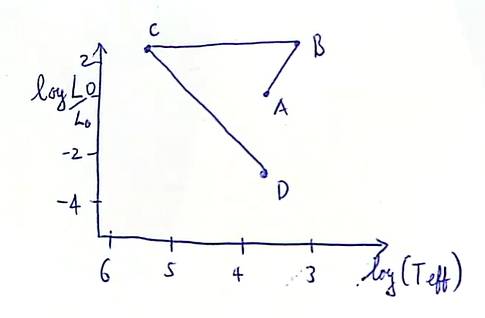
During its life a certain star goes through the following changes:
(a) Starting on the main sequence with radius R = 1 R⊙, T = 6000K (point A), the star expands and cools ending at R = 100 R⊙ and T = 3000K (point B).
(b) The star then contracts at constant luminosity to end at R = 0.01 R⊙ (point C).
(c) Finally it cools at constant radius to end at T = 6000K again (point D).
Calculate the values of log T with T in Kelvin and log(L/L⊙) for the points A, B, C and D, and hence sketch and label the stages and changes described on a Hertzsprung-Russell diagram.

Q4

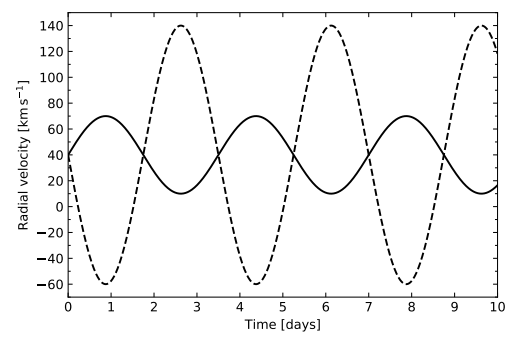
The components of a binary star are found to vary in radial velocity as shown in the figure below.
(a) Use the figure to estimate the orbital period of the binary, and the orbital speeds of each star.
(b) Use your estimates from part (a) to calculate the masses of the two stars.
(c) Why are your estimates likely to be underestimates of the true masses?
(d) Can you explain the non-zero mean radial velocity of the stars?
(e) If a Jupiter-mass exoplanet was orbiting this binary star system in a circular orbit with orbital radius 5.2 AU, what would you expect to be the effect on the measured stellar velocities?
$P = 3.5 d a y s$ , $v_{1} = 30 k m s^{- 1}$ , $v_{2} = 100 k m s^{- 1}$

\begin{aligned} ω^{2} & = G \frac{M_{1} + M_{2}}{R^{3}} \\ R & = r_{1} + r_{2} \\ v_{1} = ω r_{1} & , v_{2} = ω r_{2} \\ ω^{2} & = G ω^{3} \frac{M_{1} + M_{2}}{(v_{1} + v_{2})^{3}} \\ M_{1} + M_{2} & = \frac{(v_{1} + v_{2})^{3}}{G ω} \\ \approx 0.8 M_{⊙} \\ M_{1} r_{1} & = M_{2} r_{2} \\ M_{1} (r_{1} + r_{2}) & = (M_{1} + M_{2}) r_{2} \\ M_{1} & = (M_{1} + M_{2}) \frac{r_{2}}{r_{1} + r_{2}} \\ M_{1} & = (M_{1} + M_{2}) \frac{v_{2}}{v_{1} + v_{2}} = 0.62 M ⊙ \\ M_{2} & = 0.18 M_{⊙} \end{aligned}

Q5

The thermal energy per particle at the centre of the Sun is of order GM⊙μ/R⊙ where μ is the mean mass per particle. Assuming that this is representative of the thermal energy per particle throughout the Sun, show that the total thermal energy content of the Sun is given by $E T = \frac{G M_{⊙}^{2}}{R_{⊙}}$ . Hence calculate how many years the Sun could survive off its stored thermal energy alone at its present luminosity. This “thermal timescale” governs how long it takes a star to reach the main-sequence after its formation. Therefore explain why massive main-sequence stars form faster than low-mass main-sequence stars, as demonstrated by the absence of the latter in young star clusters.

\begin{aligned} E & = \frac{G M m}{R} \times N; N = M / p \end{aligned}