PX157 - B9 - potential gradients

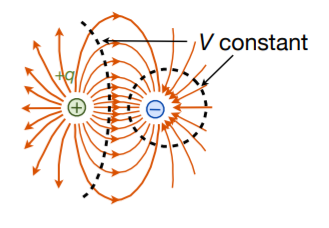
equipotential surfaces

∴ V_{a} - V_{b} = \int_{a}^{b} \vec{E} \cdot d \vec{l}

∴ V_{a} - V_{b} = \vec{E} \cdot d \vec{l}

V_{a} = V_{b} ⟹ \vec{E} \cdot d \vec{l} = 0 ⟹ \vec{E} ⊥ d \vec{l}

$d \vec{l}$ is tangential to the equipotential surface. hence, $\vec{E}$ is perpendicular to the equipotential surface
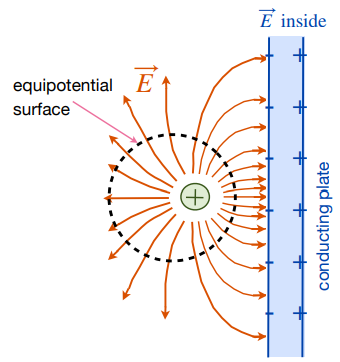
in a conductor, $\vec{E} = 0$ , and $V = c o n s t a n t ⟹$ equipotential volume

\begin{aligned} V_{a} - V_{b} & = \int_{a}^{b} \vec{E} \cdot d \vec{l} \\ V_{a} - V_{b} & = - \int_{b}^{a} d V \\ ∴ \int_{a}^{b} [\vec{E} \cdot d \vec{l} + d V] & = 0 \end{aligned}

\begin{aligned} \vec{E} \cdot d \vec{l} + d V & = 0 \\ d V & = - \vec{E} \cdot d \vec{l} \end{aligned}

d V = - {\vec{E}}_{x} d x ⟹ E_{x} = - \frac{d V}{d x}

\begin{aligned} d V = - \vec{E} \cdot d \vec{l} & = - E_{x} d x - E_{y} d y - E_{z} d z \\ = \frac{\partial V}{\partial x} d x + \frac{\partial V}{\partial y} d y + \frac{\partial V}{\partial z} d z \end{aligned}

$\vec{r} = x \hat{x} + y \hat{y} + z \hat{z}$ , and $d \vec{l} = d \vec{r} = d x \hat{x} + d y \hat{y} + d z \hat{z}$

\vec{E} = - (\frac{\partial V}{\partial x} \hat{x} + \frac{\partial V}{\partial y} \hat{y} + \frac{\partial V}{\partial z} \hat{z}) \equiv - \vec{\nabla} V

eg: a ring of charges $V (x, 0, 0) = \frac{Q}{4 π ϵ_{0} \sqrt{x^{2} + a^{2}}}$ $\vec{E} (x, 0, 0) = - \vec{\nabla} V = - (\frac{\partial V}{\partial x} \hat{x} + \frac{\partial V}{\partial y} \hat{y} + \frac{\partial V}{\partial z} \hat{z})$
- $\frac{\partial V}{\partial y} = 0$ and $\frac{\partial V}{\partial z} = 0$ because expect an extremum (minimum/maximum) on x-axis
$\begin{align*}$ &= \frac{Q}{4\pi\epsilon_{0}} \frac{x}{(x^{2}+a^{2})^{\frac{3}{2}}} \hat x
\end{align*}$$

V (r) = \frac{\vec{p} \cdot \hat{r}}{4 π ϵ_{0} r^{2}} = \frac{\vec{p} \cdot \vec{r}}{4 π ϵ_{0} r^{3}}

\vec{E} = - \vec{\nabla} V = - \frac{1}{4 π ϵ_{0}} [(\vec{p} \cdot \vec{r}) \vec{\nabla} (\frac{1}{r^{3}}) + \frac{1}{r^{3}} \vec{\nabla} (\vec{p} \cdot \vec{r})]

\begin{aligned} \vec{\nabla} (\frac{1}{r^{3}}) & = - \frac{3}{r^{4}} \vec{\nabla} r \\ = \frac{- 3}{r^{4}} \vec{\nabla} \sqrt{x^{2} + y^{2} + z^{2}} \\ = - \frac{3}{r^{4}} \frac{1}{2 \sqrt{x^{2} + y^{2} + z^{2}}} \vec{\nabla} (x^{2} + y^{2} + z^{2}) \\ = - \frac{3}{2 r^{5}} (2 x \vec{\nabla} x + 2 y \vec{\nabla} y + 2 z \vec{\nabla} z) \\ = - \frac{3}{r^{5}} (x \hat{x} + y \hat{y} + z \hat{z}) \\ = - \frac{3}{r^{5}} \vec{r} \\ ∴ \vec{\nabla} (\frac{1}{r^{3}}) & = - \frac{3}{r^{4}} \hat{r} \end{aligned}

\vec{\nabla} (\vec{p} \cdot \vec{r}) = \vec{\nabla} (p_{x} x + p_{y} y + p_{z} z) = p_{x} \hat{x} + p_{y} \hat{+} p_{z} \hat{z} = \vec{p}

\begin{aligned} \vec{E} = - \vec{\nabla} V & = - \frac{1}{4 π ϵ_{0}} [(\vec{p} \cdot \vec{r}) (- \frac{3}{r^{4}} \hat{r}) + \frac{1}{r^{3}} \vec{p}] \\ = \frac{1}{4 π ϵ_{0} r^{3}} [3 (\vec{p} \cdot \hat{r}) \hat{r} - \vec{p}] \end{aligned}