PX157 - B5b - electric field from a uniformly charged sphere
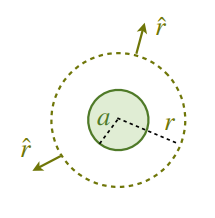
- step 1: symmetry
points radially outwards if , ie: is constant on a sphere centred on the charged sphere, ie:
- step 2: gaussian surface
- sphere of radius,
, centred on the charged sphere
\vec E \cdot d\vec S &= E , \hat r \cdot dS , \hat r = E , dS \
\therefore ;\oiint \vec E \cdot d\vec S &= \oiint E , dS = E , 4\pi r^{2}
\end{align*}$$ - sphere of radius,
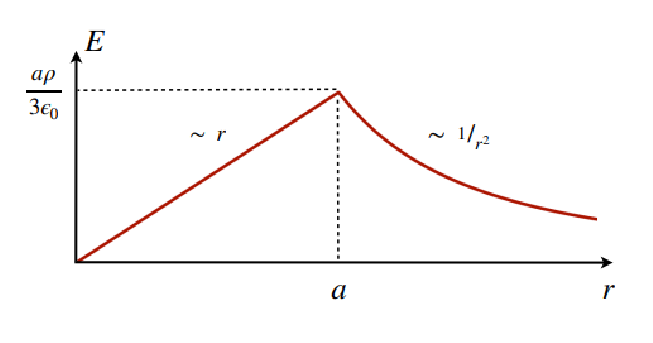
- step 3:
- if
- if
- if
- step 4:$$\begin{align*}
E , 4\pi r^{2} &= \begin{cases}
\frac{Q}{\epsilon_{0}} & r>a \
\frac{Q}{\epsilon_{0}}(\frac{r}{a})^{3} & r \leq a
\end{cases}\
E &= \begin{cases}
\frac{Q}{4\pi r^{2}\epsilon_{0}} & r>a \
\frac{Q}{4\pi a^{2}\epsilon_{0}}(\frac{r}{a}) & r \leq a
\end{cases} \
\therefore \vec E &= \begin{cases}
\frac{Q}{4\pi r^{2}\epsilon_{0}} \hat r & r>a \
\frac{Q}{4\pi a^{2}\epsilon_{0}}\left(\frac{r}{a}\right)\hat r & r \leq a
\end{cases} \
\end{align*}$$