PX155 - classical mechanics - summary

A - foundations of classical mechanics

newton's laws

first law

law of inertia
"every body continues in its state of rest or uniform motion unless acted on by an external force"

second law

"the rate of change of momentum of a body is equal to the total external force acting upon it"

F = \frac{d p}{d t}

if mass is constant:

F = m a

third law

"to every action there is an equal and opposite reaction"

friction

static friction

F_{s, m a x} = μ_{s} N

kinetic friction

F_{k} = μ_{k} N

gravitation

newton's law of gravity

{\vec{F}}_{12} = - \frac{G m_{1} m_{2}}{r^{2}} \hat{r}

newton's shell theorem

force on a mass outside the shell due to the shell is as if it is due to a point mass at the shell's centre
force on a mass inside the shell is zero as the net force is zero

B - systems of particles and acceleration

centre of mass

{\vec{r}}_{c m} = \frac{\int \vec{r} d m}{\int d m}; \int \vec{r} d m = (\int x d m, \int y d m, \int z d m)

equations of motion

constant acceleration

a = \frac{d v^{'}}{d t^{'}} : a \int_{0}^{t} d t^{'} = \int_{u}^{v} d v^{'} ⟹ a t = v - u

v = \frac{d x^{'}}{d t^{'}} : \int_{0}^{t} (u + a t) d t^{'} = \int_{0}^{s} d x^{'} ⟹ s = u t + \frac{1}{2} a t^{2}

v^{2} - u^{2} = 2 a s

time-dependent acceleration

\int_{0}^{t} a (t) d t^{'} = \int_{u}^{v} d v^{'}

position-dependent acceleration

\begin{aligned} a (x) = \frac{d v^{'}}{d t^{'}} & = \frac{d v^{'}}{d x^{'}} \frac{d x^{'}}{d t^{'}} \\ \int_{0}^{s} a (x) d x^{'} & = \int_{u}^{v} v d v^{'} \\ = \frac{1}{2} (v^{2} - u^{2}) \end{aligned}

velocity-dependent acceleration

a (v) = \frac{d v^{'}}{d t^{'}} ⟹ \int_{u}^{v} \frac{1}{a (v)} d v^{'} = t

C - work and energy

kinetic energy

K E = \frac{1}{2} m v^{2}

W = \int_{a}^{b} \vec{F} d \vec{x}

conservative forces

conservative if work done is independent of the path

\oint \vec{F} d \vec{r} = 0

W = - Δ U ⟹ Δ K E + Δ U = 0

\vec{F} = - \vec{\nabla} U

gravitational potential energy

W_{a \to b} = - G M m (\frac{1}{b} - \frac{1}{a})

Δ U = - W

considering $U_{\infty} = 0, a = \infty, b = r :$

U (r) = - \frac{G M m}{r}

gravitational potential:

ϕ = \frac{U}{m} = \frac{G M}{r}

power

P = \frac{d W}{d t} = \vec{F} \cdot \frac{d \vec{r}}{d t} = \vec{F} \cdot \vec{v}

D - simple harmonic moton

general equation

\begin{aligned} F = m a & = - k x \\ \ddot{x} + ω^{2} x & = 0; ω = \sqrt{\frac{k}{m}} \end{aligned}

∴ x = A \cos ω t + B \sin ω t

angular velocity:

ω = \frac{θ}{t}

∴ x = A \cos θ + B \sin θ

x = A^{'} \cos (ω t + ϕ)

where, $A^{'} =$ amplitude, $ϕ =$ phase angle

energy

W = \frac{1}{2} k x^{2} : U = \frac{1}{2} k A^{2} \cos (ω t)

K E = \frac{1}{2} m {\dot{x}}^{2} = \frac{1}{2} k A^{2} \sin^{2} (ω t)

E_{t o t} = \frac{1}{2} k A^{2}

complex form

x = R e (A^{'} e^{i θ} e^{i ϕ}) = R e (a e^{i ω t})

where, $a = A^{'} e^{i ϕ} =$ complex amplitude
$$\ddot z + \omega^{2} z = 0$$

damped oscillations

\begin{aligned} m \ddot{x} + b \dot{x} + k x & = 0 \\ \ddot{x} + γ \dot{x} + ω^{2} x & = 0 \end{aligned}

where, $b =$ damping coefficient, $γ = \frac{b}{m}$
$$\ddot z + \gamma \dot z + \omega^{2}z =0$$
$$\lambda = - \frac{\gamma}{2}\pm \sqrt{\left(\frac{\gamma}{2}\right)^{2}-\omega^{2}}$$

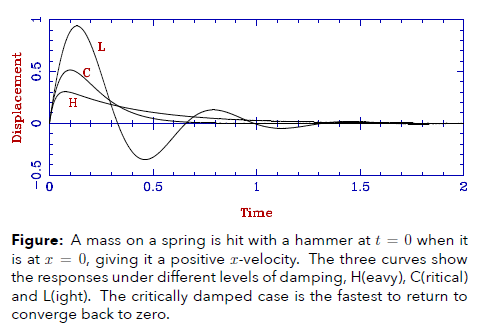
light daming

γ < 2 ω : λ = - \frac{γ}{2} \pm i ω^{'}, ω^{'} = \sqrt{ω^{2} - {(\frac{γ}{2})}^{2}}

heavy damping

γ > 2 ω : λ = - \frac{γ}{2} \pm ω^{'}, ω^{'} = \sqrt{ω^{2} - {(\frac{γ}{2})}^{2}}

critical damping

γ = 2 ω : λ = - \frac{γ}{2}

driven damped oscillations

\begin{aligned} m \ddot{x} + b \dot{x} + k x & = F_{0} \cos (ω t) \\ \ddot{z} + γ \dot{z} + ω_{0}^{2} z & = \frac{F_{0}}{m} e^{i ω t} \end{aligned}

trying $z = a e^{i ω t} :$

a = \frac{F}{m ((ω_{0}^{2} - ω^{2}) + i ω γ)} = | a | e^{i ϕ}

| a | = \frac{F}{m \sqrt{(ω_{0}^{2} - ω^{2})^{2} - (ω γ)^{2}}}; \tan ϕ = - \frac{γ ω}{ω_{0}^{2} - ω^{2}}

E - circular motion, rotation of bodies

circular motion

angular velocity ( $ω$ )

ω = \dot{θ} = \frac{2 π}{T}

\vec{v} = \vec{ω} \times \vec{r}

centripetal acceleration

a = ω v = ω^{2} r = v^{2} r

\vec{a} = a \hat{r}

moments

m o m e n t = F d_{⊥}

for a system in equilibrium, sum of moments about a point is zero

torque ( $τ$ )

\vec{τ} = \vec{r} \times \vec{F}

angular momentum

\vec{τ} = \frac{d \vec{L}}{d t}

for a particle moving in a straight line, $\vec{L}$ along any point not along the straight line $= 0$
for a lever to balance, about the fulcrum, $\vec{τ} = \frac{d \vec{L}}{d t} = 0$
for a moving particle:

\begin{matrix} \vec{L} = \vec{r} \times \vec{p} = r \times m \vec{v} \\ | \vec{L} | = m r^{2} ω \end{matrix}

orbital angular momentum

for a satellite of mass, $m$ , orbiting earth at a distance, $R$ , from the centre of earth:

\begin{array}{r} L = m R^{2} ω \\ \frac{G M m}{R^{2}} = \frac{m v^{2}}{R} \\ ∴ v = \sqrt{\frac{G M}{R}} \end{array}

\begin{aligned} \vec{τ} = \vec{R} \times \vec{F} & = 0 [∵ \vec{R} ∥ \vec{F}] \\ ∴ \frac{d \vec{L}}{d t} & = 0 \end{aligned}

angular momentum is conserved

moment of inertia (I)

I = m r^{2} ω

\vec{L} = I \vec{ω}

which is not true if:
- plane of rotation does not contain the origin of $\vec{r}$
- the origin is not the centre of rotation

K E = \frac{1}{2} m r^{2} ω^{2} = \frac{1}{2} I ω^{2}

for continuous rigid bodies

I = \int r^{2} d m

for a thin ring with radius, $R$ , and mass $M$ , about an axis perpendicular though its centre, let the mass per unit length along the circumference be $σ :$

I = R^{2} \int_{0}^{2 π} R σ d θ = 2 π R^{3} σ = M R^{2}

for a uniform disc with radius, $R$ , and mass $M$ , about an axis perpendicular though its centre:
- dividing the disc into concentric rings of radius, $r$ , and thickness, $d r$ , $σ$ is the mass per unit area such that the mass of the ring, $d m = 2 π r σ d r :$

I = \int_{0}^{R} 2 π r^{3} σ d r = \frac{1}{2} π σ R^{4} = \frac{1}{2} M R^{2}

for a hollow sphere about an axis through its centre:

I = \frac{2}{3} M R^{2}

for a solid sphere about an axis through its centre:

I = \frac{2}{5} M R^{2}

for a thin uniform rod about an axis perpendicular though its centre:

I = \frac{1}{12} M L^{2}

for a thin uniform rod about an axis perpendicular thought one end:

I = \frac{1}{3} M L^{2}

parallel axis theorem

I = I_{C O M} + m d^{2}

axes about which $I$ and $I_{C O M}$ are taken must be parallel