PX155 - B2 - continuous bodies
- more common to treat bodies as continuous, not a collection of distinct points
- eg:
and infinite number of points(elements) of mass $$\vec r_{cm}=\frac{\int \vec r dm}{\int dm}$$ - NB:
- x-component of
- NB:
- eg:
- eg: a bar of length
has mass per unit length , where is the distance from one end - to find: the position of its centre of mass
- similarly,$$\int x.dm=\int_0^L x\rho.dx =\int_o^L\alpha x^2 .dx = \alpha[\frac{x^3}{3}]_0^L= \frac{\alpha L^3}{3}$$
- hence,
- eg: find the centre of mass of a uniform semicircle of radius
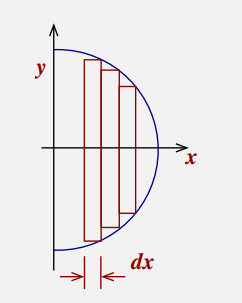
- let
- slicing the semicircle vertically:
\1\n\2\n