PX154 - I2 - polarization

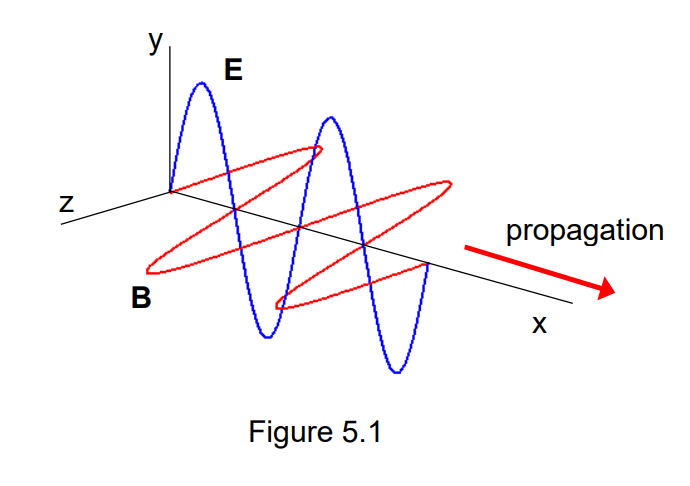
• in fig 5.1, E-field is put along the y-axis
  • in reality, it can point anywhere along the y-z plane for a wave travelling along $x$
  • B-field is ignored in fig 5.2
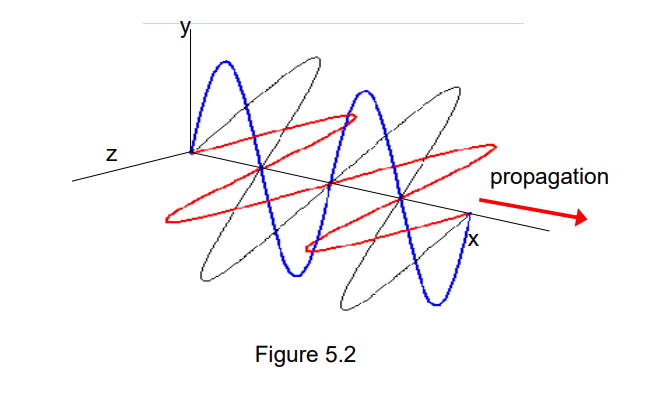
  • the components of the $\overrightarrow{E}$-field are resolved:
  $$\overrightarrow{E}(x,t)=E_y\overrightarrow{j}+E_z\overrightarrow{k}$$- eg:
  $$E_{y}= E_{0y} \cos(kx-\omega t)$$
  $$E_{z}= E_{0z} \cos(kx-\omega t)$$
  - fig 5.2 shows a wave oscillating at $45\mathrm{°}$ between $y+z$
• need to be able to have a phase difference between the components of the field:

- if $\varphi =0$: fig 5.2 - linear polarization
- if $\varphi =\frac{\pi }{2}$: fig 5.3 - circular polarization
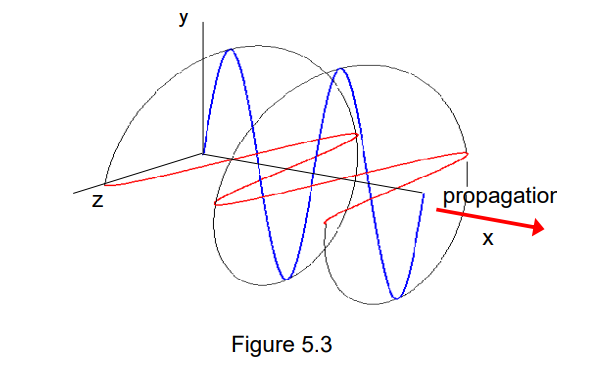
- magnitude of E-field is constant
- the E-field vector direction rotates around the x-axis, describing a helix
- left + right polarization for $\varphi =\pm \frac{\pi }{2}$
- different textbooks use opposite conventions for left + right polarization
- this is a special case of electrical polarization: when $E_{0y}\ne E_{0z}$ , or, if $\pi \ne \frac{\pi }{2}$