PX154 - H3 - standing waves and normal modes

introduction

a wave perfectly reflecting from a fixed end. now, the other end is fixed too
for sinusoidal waves:

u_{t o t a l} = A \cos (k x - ω t) - A \cos (- k x - ω t)

using trig identity:

u_{t o t a l} = 2 A \sin (k x) \sin (ω t)

- $\sin (k x)$ shows position dependence
- when $\sin (k x) = 0$ , ie $k x = n π$ , then, $u_{t o t a l}$ is always zero, for $x = \frac{1}{2} λ, λ, \frac{3}{2} λ . . .$

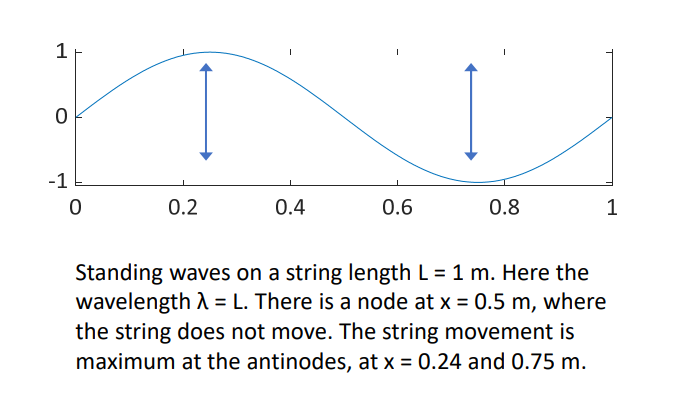
points with no vibration are nodes
points with maximum/minimum vibrations are antinodes
comments: for a standing wave there is no transfer of power

modes

a string of length, $L$ , fixed at $x = 0$ , and $x = L$
we can only have waves if $u (x, t) |_{x = L} = 0$

\begin{aligned} k x & = n π \\ x & = \frac{n λ}{2} \end{aligned}

fundamental:
$n = 1 ⟹ λ = 2 L$
$f = \frac{v}{2 L}$
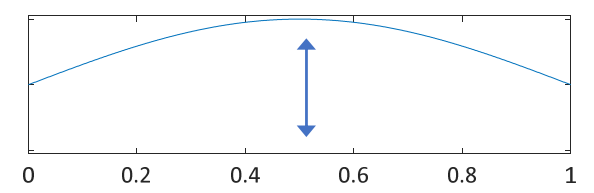
first harmonic:
$n = 2 ⟹ λ = L$
$f = \frac{v}{L}$
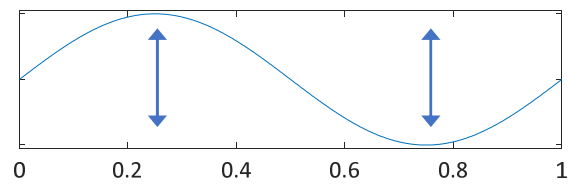
second harmonic:
$n = 3 ⟹ λ = \frac{2}{3} L$
$f = \frac{3 v}{2 L}$
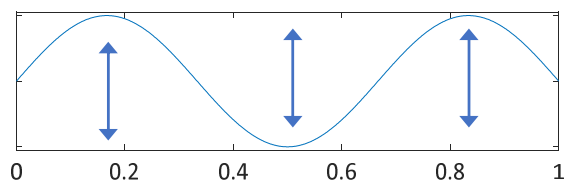
third harmonic:
$n = 4 ⟹ λ = \frac{1}{2} L$
$f = \frac{2 v}{L}$
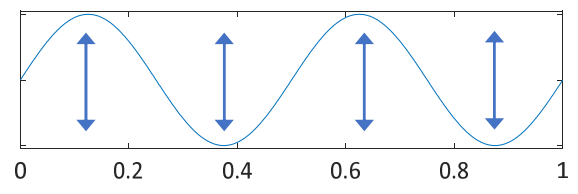
more in [YF fig 40.11]
power in the wave:

P = \frac{1}{2} A^{2} ω^{2} z \propto f^{2}

- the higher modes are more energetic
- the wavelengths, frequencies, and energies are quantized
- if a note is played on a piano, the fundamental and combinations of harmonics is produced - requires [fourier analysis]

waves in open pipes

[YF 16.4]

check this
for a both-ends-open pipe, the density and pressure of air at the ends are fixed by the room conditions.
- density and pressure at the ends of the pipe remain constant, which gives the boundary condition
- standing waves are obtained