PX154 - G1a - waves on a taut string

[YF 15.4 "second method"]

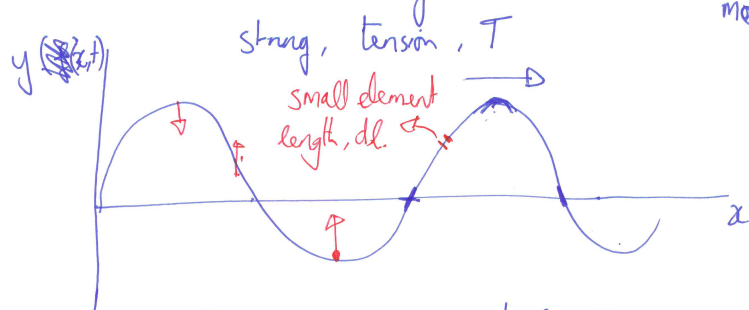
• string with a mass per unit length, $\mu$

• consider a transverse wave propagating along the string

  • oscillations of the string are only along the y-direction (no physical motion along the x-direction)

• we analyse the behaviour of a small element
  

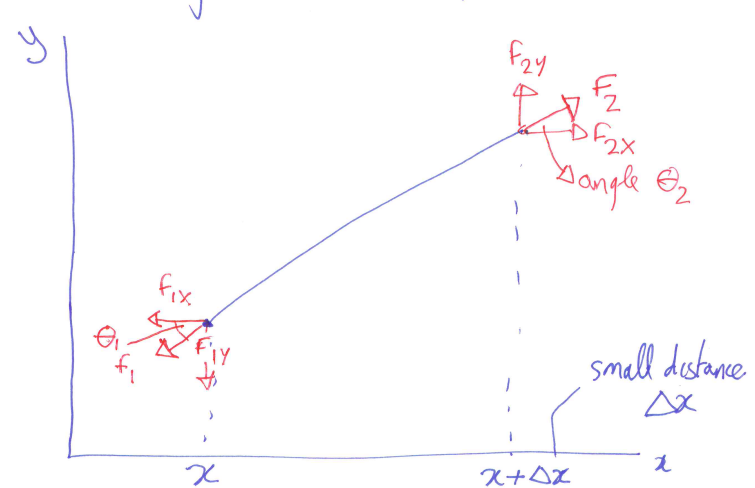
• this is a flexible string, ie: forces can only act along the string itself

• originally, we have tension, $T$, in the string

• motion of the string is only along the y-direction

  • therefore, $F_{1x}$ and $F_{2x}$ should be equal and opposite to each other
  • no net force, hence no acceleration, along the x-direction
  • we set $F_{1x}=F_{2x}=T$

• there will be components of force along the y-direction with a resultant force (unless the string is straight, ie: ${\theta }_1={\theta }_2$)

  • there is a net force along $y$
  • at x,
  $$F_{1y}=F_{1x}\tan {\theta }_1$$

  - acting downwards

  • writing it in terms of gradient:
  $$F_{1y}=F_{1x}{\left(\frac{dy}{dx}\right)}_x$$
  • at $x+\mathrm{\Delta }x$:
  $$F_{2y}=F_{2x}\tan {\theta }_2$$

  - writing in terms of the gradient:
  $$F_{2y} = F_{2x} \left(\frac{dy}{dx}\right)_{x+dx}$$

  • net force acting upwards:
  $$F_y=F_{2y}-F_{1y}$$

  - if $F_y\ne 0$, then there will be an acceleration along the y-direction, since $F=ma$, where $a=\frac{d^{2}y}{d{x}^2}$
  - for mass, we use $m=\mu x$

  • hence:
  $$F_y=\mu \mathrm{\Delta }x\frac{d^{2}y}{d{x}^2}=F_{2y}-F_{1y}$$
  • remember $F_{1x}=F_{2x}=T$:
  $$\mu \mathrm{\Delta }x\frac{d^{2}y}{d{x}^2}=T({\left(\frac{dy}{dx}\right)}_{x+\mathrm{\Delta }x}-{\left(\frac{dy}{dx}\right)}_x)$$$$\mu \frac{{\partial }^{2}y}{\partial t^2}=\frac{T({\left(\frac{\partial y}{\partial x}\right)}_{x+\mathrm{\Delta }x}-{\left(\frac{\partial y}{\partial x}\right)}_x)}{\mathrm{\Delta }x}$$
  • let $\mathrm{\Delta }x\to 0$:
  $$\frac{{\partial }^{2}y}{\partial t^2}=\frac{T}{\mu }\frac{{\partial }^{2}y}{\partial x^2}$$

  - this is a wave equation
  - comparing with the wave equation, we see
  $$v = \sqrt{\frac{T}{\mu}}$$

  • comments:
    • this is a simple model
      • we could account for the stretching of the string
      • we could account for stiffness (perhaps a metal wire)
      • or consider the 'bead model' for wavelengths approaching distance between atoms in solids. [Y2, Y3: phonons]