PX154 - E5 - reversible and irreversible processes

heat transfers

consider a heat engine placed next to a cold engine
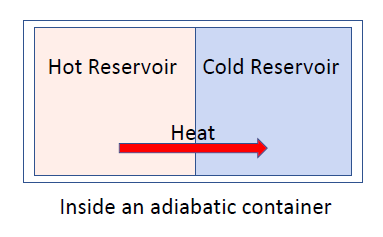
initially, the objects are not in equilibrium and heat is transferred from hot $\to$ cold until they have the same temperature
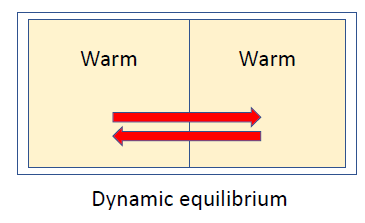
heat will not be transferred to return to the first state of hot and cold, so, the process is irreversible

in the study of the carnot cycle, an isothermal expansion was first considered
if the reservoir is the same temperature as the engine ( $T_{H}$ ), then there is no heat transfer, so, $Q_{H} = 0$ , and nothing happens! ( $W = 0$ )
set $T_{e n g i n e} < T_{H}$ in order to obtain $Q_{H} \neq 0$ , but this is no longer reversible since heat is transferred from warmer reservoir to the cooler engine
for an isothermal process an infinitesimally small difference in temperature is required so that the process could be reversed by an infinitesimally small change in conditions
process has to be slow so that the engine can always be considered to be in equilibrium
why does this matter?
- if $T_{H} > T_{e n g i n e}$ then $Q_{H} + v e$ , and some of $Q_{H}$ will go to work done, however, some of the heat, $Q_{H}$ , will warm the engine
- so, the work done, $W$ , is reduced, which reduces efficiency
- therefore, the reversible isotherm gives the maximum $W$ for a given $Q_{H}$
adiabatic cooling (step $B \to C$ in the carnot cycle)
- still an expansion: engine doing work
- cooling from $T_{H} \to T_{C}$
- $T_{e n g i n e}$ is not known at any given time, but $T_{e n g i n e} > T_{C} :$ heat transfer to reservoir cannot be allowed to occur as this would be irreversible
- if $Q_{C} = 0$ , then again $W$ is maximized
- if $Q_{C} \neq 0$ , energy is lost to the reservoir reducing efficiency

the most efficient cycle is reversible and consists of isotherms and adiabats
however, all real processes are irreversible and proceed in a particular direction
- the first law doesn't tell this
- the second law of thermodynamics does