PX154 - C9 - heat capacity of the ideal gas

[YF 18.6]

relating heat capacity

• need to relate the heat capacity of our gas to its motion (the motion of its molecules)
• two definitions to consider:
  • $C_v=$ heat capacity at constant volume
  • $C_p=$ heat capacity at constant pressure

heat capacity at constant volume

• for now, consider $C_V$:

• if some heat, $Q$, is added, the kinetic energy of the gas increases:

• from here:

• for $N$ molecules:

• and for $n$ moles:

• $K_{tr}$ used instead of ${\overline{E}}_K$ - kinetic energy owing to translation

• at $STP$, measured values:

• key observations:
  • noble gases - monatomic $:C_V\approx \frac{3}{2}R$
  • other - diatomic $:C_V\approx \frac{5}{2}R$
• reason:
  • monatomic particles only translation
  • for diatomic, there may be rotation and vibration

equipartition of energy

• each form of motion is a "degree of freedom" and contributes to $\frac{1}{2}{k}_{B}T$ of energy per atom

translation

[YF 18.18]

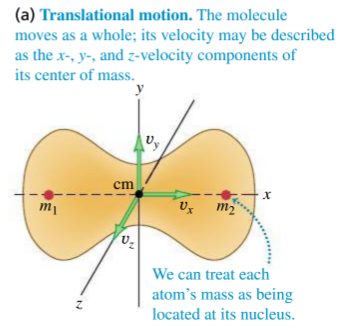
• our translation is in 3D, and translation in each of these is a degree of freedom contributing $\frac{1}{2}{k}_{B}T$
• translation in 3D contributes to a total energy $\frac{3}{2}{k}_{B}T$ per atom
• for $n$ moles, $\frac{3}{2}nRT$ :

rotation

• neglect this for monatomic gases
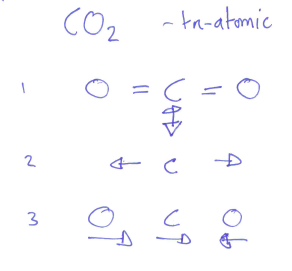
• diatomic gases:
  • molecule can rotate, but not about all 3 axes:
    [YF 18.18]
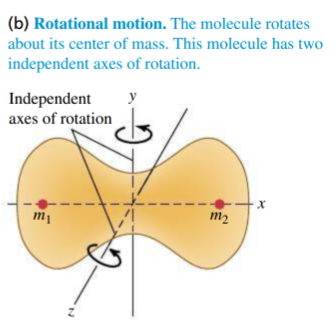
  • it is found that rotation can only be observed about $y$ and $z$ axes
  • one of these axes is along the molecule's axis, effectively the same as the monatomic case, so there is no contribution
  • this gives 2 degrees of freedom
    • $2\times \frac{1}{2}{k}_{B}T=k_{B}T$ per atom $=RT$ per mole
  • for $C_V$, an extra $R$ is obtained
  $$\therefore C_{V}fortranslationandrotation=\frac{5}{2}R$$

vibration

• doesn't exist for monatomic molecules

• molecules can vibrate via stretching/contracting, or sometimes by bending of the interatomic bonds

• the bond can be modelled as a spring and treat it as a harmonic oscillator, SHM
  [YF 18.18]

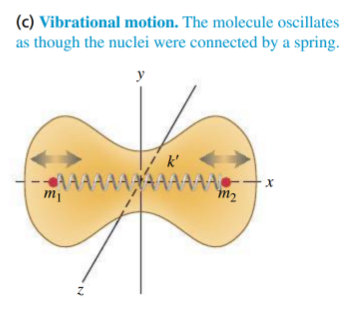
• $KE$ and $PE$ from the vibration have to be included. each adds one degree of freedom

  • total $k_{B}T$
  • contribution to $C_V$ is $Rpermole$

• at room temperature, vibration doesn't contribute to the heat capacity

• vibration is quantized

  • requires a quantum mechanical model PX262 - 0 - quantum mechanics and its applications
  • eg: for $N_2$, minimum energy to be absorbed to increase vibration is $0.3eV$
  • using $k_{B}T$, this corresponds to a temperature of $3000K$

• [YF fig 18.19]

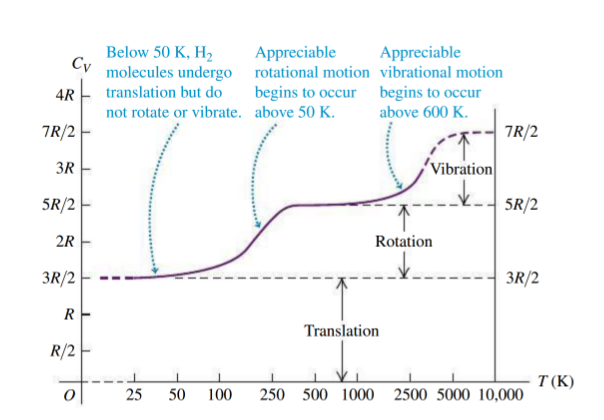
• comment:

  • for larger molecules, vibrations are more complicated with different modes available
  • 
  • $C{O}_2$ at $STP:C_V=28.5Jmo{l}^{-1}{K}^{-1}$