PX154 - C6 - kinetic-molecular model of the ideal gas

derivation

how collisions of the molecule lead to pressure
consider a volume of $V$ filled with an ideal gas of $N$ molecules, each of mass $m$
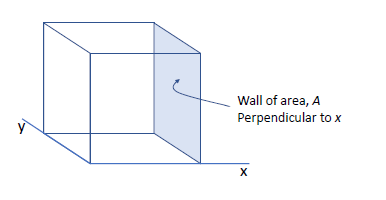
firstly, consider just one molecule of gas moving in 3D with a velocity of $\vec{v}$
consider an elastic collision with the shaded wall
in the collision, $x$ component is reversed but $y$ and $z$ components are unchanged
the change in momentum is then $2 m v_{x}$
we need to know the rate at which collisions occur with the wall for the gas
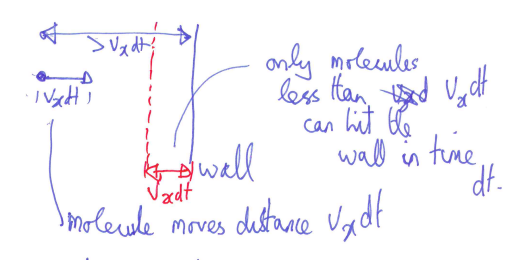
how many molecules hit the wall in a time $d t$ ?
molecules have an x-component of velocity $v_{x}$
in time $d t$ , they can move a direction of $v_{x} d t$ , so, only molecules less than $v_{x} d t$ can hit the wall

n_{c o l} = \frac{1}{2} \frac{N}{V} A v_{x} d t

- where, $V =$ number density

only half the molecules are likely to be moving towards the wall at given time $∴ \frac{1}{2}$
so, change in momentum $d Q$ in time $d t$ :

d Q = n_{c o l} 2 m v_{x} = \frac{N}{V} A m v_{x}^{2} d t

F = \frac{d Q}{d t} = \frac{N}{V} A m v_{x}^{2}

p = \frac{F}{A} = \frac{N}{V} m v_{x}^{2}

we apply the same argument for $v_{y}$ and $v_{z}$
in an isotropic system, $v_{x} = v_{y} = v_{z}$ , ie: $v^{2} = v_{x}^{2} + v_{y}^{2} + v_{z}^{2}$ :

p = \frac{1}{3} \frac{N}{V} m v^{2}

we have assumed that all $m$ molecules have the same speed $v$ , however, we will see that the molecules have a distribution of speeds here
here, we are using $v^{2}$ , so, we will use the average value of $v^{2 ⟹} {\bar{v}}^{2}$

p = \frac{N}{3 V} m {\bar{v}}^{2}

p V = \frac{1}{3} N m {\bar{v}}^{2} = N k_{B} T

$Δ p = 2 m v_{x}$
PX155 - A2 - newton's second law: $F = \frac{2 m v_{x}}{d t}$

if length of the cube is $L$ , time for a molecule to get from one wall to the other and back:
$v_{x} = \frac{2 L}{d t} ⟹ d t = \frac{2 L}{v_{x}}$
$⟹ F = \frac{m v_{x}^{2}}{L}$
for $N$ molecules: $\frac{F}{N} = \frac{m {\bar{v}}_{x}^{2}}{L}$

p = \frac{F}{A} = \frac{\frac{N m {\bar{v}}_{x}^{2}}{L}}{A} = \frac{m {\bar{v}}_{x}^{2}}{V}

statistically, ${\bar{v}}^{2} = {\bar{v}}_{x}^{2} + {\bar{v}}_{y}^{2} + {\bar{v}}_{z}^{2} = 3 {\bar{v}}_{x}^{2}$

⟹ p V = \frac{1}{3} N m {\bar{v}}^{2}

\frac{3}{2} p V = N \frac{1}{2} m {\bar{v}}^{2} = N k_{B} T

[YF p619]

T = \frac{m {\bar{v}}^{2}}{3 k_{B}}

- microscopic definition of temperature

m {\bar{v}}^{2} = 3 k_{B} T

{\bar{E}}_{K} = \frac{3}{2} k_{B} T

- we have related the average KE of the gas to its temperature